PROBLEM LINK:
Author: Jafar Badour
Tester & Editorialist: Hussain Kara Fallah
PROBLEM EXPLANATION
You are given n black points and m white points in 2D plane. You need to draw a line that separates both of these groups. In other words, all-white points must lie onto one side of the line, and the black points must be on the other side. You need to find a line with maximum thickness, or state that it’s impossible to draw any line.
n,m \leq 10^5
DIFFICULTY:
Hard
Quick Explanation
Find the convex hull for each set of points, denote black hull by A and white hull by B. Find Minkowski sum of (A - B) and check the point with minimum distance to the origin. If the origin is inside the Minkowski sum polygon then answer is -1
EXPLANATION:
First of all, let’s find the convex hull for white points and denote it by A and the convex hull of black points and denote it by B.
If A has a non-zero area of intersection with B it means that it’s impossible to draw any line.
Let’s think of possible cases of our line. The first thing that may come across the mind is that our line would be orthogonal to some line segment connecting a black point and a white point. If the line is not orthogonal it means that it’s closer to one point more than the other one, and we can rotate it such that we balance the difference (and make both distances equal).
Which pair of points should we consider? Obviously the closest pair of (black-white) points. If we pick another pair let’s say (P_x,P_y) and the closest pair is (P_a,P_b) and we draw a line with a thickness equal to the distance between P_x and P_y then (P_a,P_b) are definitely inside our thick line (which is not acceptable).
There are 2 other possible cases which we must consider.
The closest black point to the convex hull of white points A. (The segment here would be between a black point and some edge of A). Our line would be orthogonal to this segment of course.
The closest white point to the convex hull of black points B.
We should calculate the minimum distance for each of the 3 cases and take the minimum result possible.
Such a solution is possible with a radial sweep. The solutions is kind of complicated but there’s a much cleaner solution with Minkowski sum.
Minkowski sum of 2 shapes A,B in any dimensional space is the set of points:
A \oplus B=\{p + q | p \in A, q\in B\}
So basically it’s the convolution between 2 polygons. Maybe it’s a little bit hard to visualize it. Check these pictures for better understanding.
Convolution between a polygon and a triangle:


Convolution between a polygon and a circle:


It should be clear that convolution between A and -B would give us all vectors between each point in A and each point in B .
Minkowski sum between 2 convex polygons is a convex polygon. If we are able to find the vertices of Minkowski sum of A-B then our answer would be the closest point between our polygon and the origin (0,0)
How to find Minkowski sum of 2 convex polygons?

Here I will provide a short proof of the algorithm. Assume we are working with 2 convex polygons P,R and their minkowski sum P \oplus R
An extreme point in direction d on P \oplus R is the sum of extreme points in direction d on P and R.
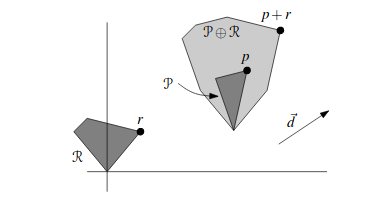
To see that the complexity of the Minkowski sum is linear, consider an edge e of P \oplus R. This edge is extreme in the direction of its outer normal. Hence, it must be generated by points on P and R that are extreme in the same direction. Moreover, at least one of P and R must have an edge that is extreme in that direction. We charge e to this edge. This way each edge is charged at most once, so the total number of edges is at most n+m.
What our algorithm does is determining the angular interval for each edge of each polygon such that this edge is extreme on this interval.
All that’s remaining is finding the distance between the origin and each edge of minkowski sum polygon.
AUTHOR’S AND TESTER’S SOLUTIONS:
Implementation: Can be found here