PROBLEM LINK:
Setter: Alei Reyes
Tester: Teja Vardhan Reddy
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy
PREREQUISITES:
Basic Math, Greedy
PROBLEM:
Chef Ada is building a new restaurant in the following way:
- First, N points X_1, X_2, \ldots, X_N are chosen on the x-axis.
- Then, N columns (numbered 1 through N) are made. For simplicity, the columns are represented as vertical segments; for each valid i, the height of the i-th segment is H_i.
- Ada assigns a column to each of the points X_1, X_2, \ldots, X_N in an arbitrary way (each column must be assigned to exactly one point).
- Finally, Ada constructs the roof of the restaurant, represented by a polyline with N vertices. Let’s denote the column assigned to the i-th point by P_i. For each valid i, the i-th of these vertices is (X_i, H_{P_i}), i.e. the polyline joins the tops of the columns from left to right.
Ada wants the biggest restaurant. Help her choose the positions of the columns in such a way that the area below the roof is the biggest possible. Formally, she wants to maximise the area of the polygon whose perimeter is formed by the roof and the segments (X_N, H_{P_N}) - (X_N, 0) - (X_1, 0) - (X_1, H_{P_1}). Let S be this maximum area; you should compute 2 \cdot S (it is guaranteed that 2 \cdot S is an integer).
QUICK EXPLANATION
- For p-th column, the contribution to area is independent to the heights of adjacent columns, only depending upon X_{min(p+1, N)} and X_{max(1, p-1)} (min and max cases for border positions.)
- For column at position p, contribution to area is H_i*(X_{min(p+1, N)} - X_{max(1, p-1)}). Let’s define v_i = X_{min(p+1, N)} - X_{max(1, p-1)} for 1 \leq i \leq N. So we need to find maximize \sum_{i = 1}^N H_i*v_i by permuting H
- In order to maximize, it is optimal to pair largest v_i with largest H_i, second largest v_i with second largest H_i and so on.
EXPLANATION
Let us compute the area below the roof for the given columns. Refer to the following image. (Triangulation to ease calculation of area and Referring i-th column by H_i)
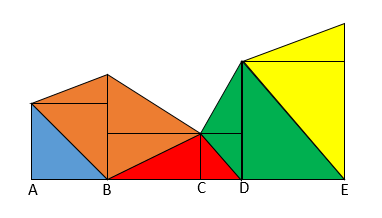
- Area of blue region is H_1*(B-A)/2 since it’s a right triangle.
- Area of orange region is H_1*(B-A)/2 + (H_2-H_1)*(B-A)/2 + H_3*(C-B)/2+(H_2-H_3)*(C-B)/2 which can be written as H_2*(B-A)/2+H_2*(C-B)/2 which is H_2*(C-A)/2
- Area of Red region is H_3*(C-B)/2+H_3*(D-C)/2 which is same as H_3*(D-B)/2
- Area of Green region is H_3*(D-C)/2+(H_4-H_3)*(D-C)/2+H_4*(E-D)/2 which is H_4*(E-C)/2
- Area of yellow region is H_4*(E-D)/2+(H_5-H_4)*(E-D)/2 which is H_5*(E-D)/2
As we can see, we can split the total area under polyline into a sum of N different terms, i-th term being dependent only on H_i, hence we can calculate the contribution of each column into total area independent of heights or positions of other columns.
Also, Contribution of p-th column is given by H_p*(X_{p+1}-X_{p-1}) if p is not at either end. If it is at left end, then contribution is given as H_p*(X_{p+1}-X_p) and if it is right end, then contribution is given by H_p*(X_p-X_{p-1})
Now, let’s define v_p = X_{min(p+1, N)}-X_{max(p-1, 1)}. So our problem becomes to choose a permutation of H so as to maximize \sum_{i = 1}^{N} H_i*v_i which is same as pairing each H_p with some v_i.
Now, let us consider a different problem.
Suppose we have two sets \{a, b\} and \{c, d\} such that a > b and c > d and we need to match each element in the first set with a different element of the second set. The value of pairing is the sum of the product of value of each pair.
We can see, two pairings possible, pairing a with b and c with d, OR pairing a with d and b with c. We need to find wich one is greater, a*b+c*d or a*d+b*c
Let’s write a = b+x and c = d+y, a*b+c*d become 2*c*d+c*y+d*x+x*y and a*d+b*c become 2*c*d+d*x+c*y. We can see that first term exceed second term by x*y which is positive since x, y > 0
So, it is optimal to pair large values in the first set with large value in the second set.
Coming back to our problem, we can generalize this, we can find that pairing the largest height column with the largest elements of v gives the maximum area.
Hence, we can compute v array, sort both v and H and compute the total area, thus computing the maximum area.
TIME COMPLEXITY
The time complexity is O(N*log(N)) per test case.
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
typedef long long int uli;
int rint(char nxt){
char ch=getchar();
int v=0;
int sgn=1;
if(ch=='-')sgn=-1;
else{
assert('0'<=ch&&ch<='9');
v=ch-'0';
}
while(true){
ch=getchar();
if('0'<=ch && ch<='9')v=v*10+ch-'0';
else{
assert(ch==nxt);
break;
}
}
return v*sgn;
}
int main(){
// freopen("2.in","r",stdin);
// freopen("2.out","w",stdout);
int t=rint('\n');
assert(1<=t&&t<=3e5);
int sn=0;
while(t--){
int n=rint('\n');
sn+=n;
assert(sn<=1e6);
assert(2<=n && n<=1e5);
vector<int>x(n),h(n);
for(int i=0;i<n;i++){
x[i]=rint(' ');
h[i]=rint('\n');
assert(0<=x[i]&&x[i]<=2e9);
assert(1<=h[i]&&h[i]<=1e9);
}
for(int i=1;i<n;i++)assert(x[i]>x[i-1]);
vector<int>d(n,0);
for(int i=0;i<n;i++){
if(i+1<n)d[i]=x[i+1]-x[i];
if(i-1>=0)d[i]+=x[i]-x[i-1];
}
sort(d.begin(),d.end());
sort(h.begin(),h.end());
uli ans=0;
for(int i=0;i<n;i++)ans+=uli(d[i])*uli(h[i]);
printf("%lld\n",ans);
}
assert(getchar()==EOF);
return 0;
}
Tester's Solution
//teja349
#include <bits/stdc++.h>
#include <vector>
#include <set>
#include <map>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <climits>
#include <utility>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <iomanip>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
//setbase - cout << setbase (16); cout << 100 << endl; Prints 64
//setfill - cout << setfill ('x') << setw (5); cout << 77 << endl; prints xxx77
//setprecision - cout << setprecision (14) << f << endl; Prints x.xxxx
//cout.precision(x) cout<<fixed<<val; // prints x digits after decimal in val
using namespace std;
using namespace __gnu_pbds;
#define f(i,a,b) for(i=a;i<b;i++)
#define rep(i,n) f(i,0,n)
#define fd(i,a,b) for(i=a;i>=b;i--)
#define pb push_back
#define mp make_pair
#define vi vector< int >
#define vl vector< ll >
#define ss second
#define ff first
#define ll long long
#define pii pair< int,int >
#define pll pair< ll,ll >
#define sz(a) a.size()
#define inf (1000*1000*1000+5)
#define all(a) a.begin(),a.end()
#define tri pair<int,pii>
#define vii vector<pii>
#define vll vector<pll>
#define viii vector<tri>
#define mod (1000*1000*1000+7)
#define pqueue priority_queue< int >
#define pdqueue priority_queue< int,vi ,greater< int > >
#define flush fflush(stdout)
#define primeDEN 727999983
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
// find_by_order() // order_of_key
typedef tree<
int,
null_type,
less<int>,
rb_tree_tag,
tree_order_statistics_node_update>
ordered_set;
#define int ll
int x[123456],h[123456];
main(){
std::ios::sync_with_stdio(false); cin.tie(NULL);
int t;
cin>>t;
while(t--){
int n;
cin>>n;
int i;
rep(i,n){
cin>>x[i]>>h[i];
}
sort(h,h+n);
vi vec;
vec.pb(x[1]-x[0]);
vec.pb(x[n-1]-x[n-2]);
f(i,1,n-1){
vec.pb(x[i+1]-x[i-1]);
}
int ans=0;
sort(all(vec));
rep(i,n){
ans+=vec[i]*h[i];
}
cout<<ans<<endl;
}
return 0;
}
Editorialist's Solution
import java.util.*;
import java.io.*;
import java.text.*;
class BIGRES{
//SOLUTION BEGIN
void pre() throws Exception{}
void solve(int TC) throws Exception{
int n = ni();
long[] x = new long[n], h = new long[n];
for(int i = 0; i< n; i++){
x[i] = nl();
h[i] = nl();
}
long[] v = new long[n];
for(int i = 0; i< n; i++)v[i] = x[Math.min(i+1, n-1)]-x[Math.max(i-1, 0)];
Arrays.sort(v);
Arrays.sort(h);
long ans = 0;
for(int i = 0; i< n; i++)ans += v[i]*h[i];
pn(ans);
}
//SOLUTION END
void hold(boolean b)throws Exception{if(!b)throw new Exception("Hold right there, Sparky!");}
DecimalFormat df = new DecimalFormat("0.00000000000");
static boolean multipleTC = true;
FastReader in;PrintWriter out;
void run() throws Exception{
in = new FastReader();
out = new PrintWriter(System.out);
//Solution Credits: Taranpreet Singh
int T = (multipleTC)?ni():1;
pre();for(int t = 1; t<= T; t++)solve(t);
out.flush();
out.close();
}
public static void main(String[] args) throws Exception{
new BIGRES().run();
}
int bit(long n){return (n==0)?0:(1+bit(n&(n-1)));}
void p(Object o){out.print(o);}
void pn(Object o){out.println(o);}
void pni(Object o){out.println(o);out.flush();}
String n()throws Exception{return in.next();}
String nln()throws Exception{return in.nextLine();}
int ni()throws Exception{return Integer.parseInt(in.next());}
long nl()throws Exception{return Long.parseLong(in.next());}
double nd()throws Exception{return Double.parseDouble(in.next());}
class FastReader{
BufferedReader br;
StringTokenizer st;
public FastReader(){
br = new BufferedReader(new InputStreamReader(System.in));
}
public FastReader(String s) throws Exception{
br = new BufferedReader(new FileReader(s));
}
String next() throws Exception{
while (st == null || !st.hasMoreElements()){
try{
st = new StringTokenizer(br.readLine());
}catch (IOException e){
throw new Exception(e.toString());
}
}
return st.nextToken();
}
String nextLine() throws Exception{
String str = "";
try{
str = br.readLine();
}catch (IOException e){
throw new Exception(e.toString());
}
return str;
}
}
}
Feel free to share your approach. Suggestions are welcomed as always. ![]()

