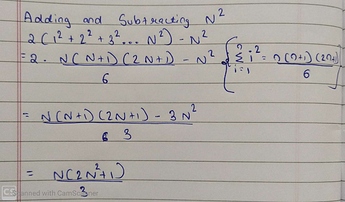Contest Link : Project Code 1.0
Problem: More Cake
Problem setter: @mohilllll
Logic (Explanation)
We get the following things as input:
- T: Number of families in the locality.
- S: Number of slices baked per family.
- N: Number of members in a particular family.
- K: Slices received by the smallest member of the family.
- R: Lucky number of the family.
Let’s talk about each family first, the youngest family member gets K slices. Member older than them would get K.R slices, now the next member would get RRR times slices more than the previous one i.e. K.R.R slices.
We can see a series being formed where the next term exceeds the previous by RRR times. This series is called Geometric Progression.
Example
Example
For example, For a family of N = 4 members, the smallest member getting K = 2 slices and R = 3. The family made S = 100 slices. We get,
- The first member gets 2 slices.
- The second member gets 2*3 = 6 slices.
- The third member gets 6*3 = 18 slices.
- Fourth member gets 18*3 = 54 slices.
- The sum would be 80 slices.
It is known that sum of finite GP is given by \frac{A(F^N -1)}{F - 1} , where A is the first element of the series, F is the common ratio and N is the number of elements.
In this question, A is K, F is R, and the number of elements would be the number of family members i.e. N.
There is a special case for it! Can you think of it?
Special Case
If R = 1, the denominator would become zero which isn’t right, so in that case, required slices would be N.K
Now if the sum of GP ≤ S, add S - Sum of GP to a variable extraSlices, otherwise add Sum of GP - S to variable requiredSlices. Do this for T families and then,
If requiredSlicess ≤ extraSlices print POSSIBLE else print IMPOSSIBLE.
Setter's Solution in Python
def gpSum(a, r, n):
ans = (a*(r**n - 1))//(r-1)
return ans
totalSlices = 0
totalReq = 0
for t in range(int(input())):
s, n, k, r = map(int, input().split())
if r == 1:
temp = k*n
else:
temp = gpSum(k, r, n)
if temp > s:
print("IMPOSSIBLE", temp-s)
else:
print("POSSIBLE", s-temp)
totalSlices += s
totalReq += temp
if totalSlices<totalReq:
print('IMPOSSIBLE')
else:
print('POSSIBLE')
Problem: Punish Alex
Problem setter: @prasukj
Logic (Explaination)
The question can be modeled as a simple problem involving a
a little bit of mathematics.
Firstly we check whether k<n; if it is then the answer is directly k
else if k>n; then we try to find out the position of the person on the staircase.
We store the tentative position in a temp variable using the equation:-
temp=(k-n)%(n-1)
Then we try to find the number of times the person covered all the stairs with the following equation:-
(k-n)/(n-1)
We do this to find the position where the person will start climbing or be coming down.
if the above equation is odd(the person is at the lower end) the final position is temp+1 otherwise(the person is at the upper end) it is n-temp.
Setter's Solution in Python
for t in range(int(input())):
n, k = map(int, input().split())
if k <= n:
print(k)
else:
k -= n
quo = k//(n-1)
rem = k%(n-1)
if quo%2:
print(rem+1)
else:
print(n-rem)
Problem: Lord of the Rings
Problem setter: @hk2098
Logic (Explanation)
It can be observed that all the pairs are formed when the second number (y) is entirely made of digit 9
We have to find the total number of y that can be formed with only 9
The answer to that is [Log10(N+1)] i.e the integer value of Log10(N+1)
Log10(N) gives us the total number of digits in N minus 1.
Using (N+1) takes care of the cases where y is made of 9
Eg: 9999 becomes 10000 so [Log10(N+1)] gives us 4, so we include 9999 in the list
So the total number of numbers that can be formed with the only digit 9 is
[Log10(N+1)]
Let D=[Log10(N+1)]
All the numbers up to N can be paired with D numbers
Therefore, the total number of pairs is x X D
The unique pairs are all the values of x up to N
Therefore;
The unique values of x would be M
The total number of pairs would be M X D
Setter's Solution in Python
for t in range(int(input())):
n, k = map(int, input().split())
if k <= n:
print(k)
else:
k -= n
quo = k//(n-1)
rem = k%(n-1)
if quo%2:
print(rem+1)
else:
print(n-rem)
Problem: Love Polygons
Problem setter: @phoenix_307
Logic (Explanation)
The question can be modeled as an undirected graph
where each person is a node and
for each person, there is an undirected edge between
them and the person they like.
Then the question is simply reduced to finding the total number of connected components.
As the people in a particular polygon will always have some
direct/indirect connection amongst themselves
The no. of connected components can be found by simply
doing DF from an unvisited node and marking all the reachable nodes as visited.
In a single DFS, all the nodes in a particular love polygon will be marked visited.
We can do this until all nodes have been visited.
Setter's Solution in Python
#from time import time
def solve(graph):
grps = []
n = len(graph)
vis = [False for i in range(n)]
for i in range(n):
if not vis[i]:
ct = 0
vis[i] = True
wait = [i]
while(wait):
currNode = wait.pop()
ct += 1
for node in graph[currNode]:
if not vis[node]:
vis[node] = True
wait.append(node)
grps.append(ct)
return sorted(grps)
#tic = time()
for t in range(int(input())):
n = int(input())
graph = dict(zip(range(n), [[] for i in range(n)]))
for i in range(int(input())):
src, dest = map(int, input().split())
graph[src].append(dest)
graph[dest].append(src)
groups = solve(graph)
print(len(groups))
print(*groups)
#toc = time()
#print(toc - tic)
Setter's Solution in Java
import java.io.*;
import java.math.*;
import java.util.*;
public class Main {
private static Scanner sc;
public static void main(String args[]) {
sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- > 0) {
int n = sc.nextInt();
ArrayList<ArrayList<Integer>> adj = new ArrayList<ArrayList<Integer>>(n);
for (int i = 0; i < n; i++)
adj.add(new ArrayList<Integer>());
int q = sc.nextInt();
for (int i = 0; i < q; i++) {
int a1 = sc.nextInt();
int a2 = sc.nextInt();
addEdge(adj, a1, a2);
//addEdge(adj, a2, a1);
}
int size = 0;
int groups[] = new int[n];
boolean vis[] = new boolean[n];
for (int i = 0; i < n; i++) {
if (vis[i] == false) {
int ct = 0;
vis[i] = true;
Stack<Integer> wait = new Stack<>();
wait.push(i);
while (!wait.isEmpty()) {
int cn = wait.pop();
ct++;
for (int node = 0; node < adj.get(cn).size(); node++) {
if (vis[adj.get(cn).get(node)] == false) {
vis[adj.get(cn).get(node)] = true;
wait.add(adj.get(cn).get(node));
}
}
}
groups[size++] = ct;
}
}
Arrays.sort(groups);
System.out.println(size);
for (int i = n - size; i < n; i++) {
System.out.print(groups[i] + " ");
}
System.out.println();
}
}
static void addEdge(ArrayList<ArrayList<Integer>> adj, int u, int v) {
adj.get(u).add(v);
//adj.get(v).add(u);
}
}
Setter's Solution in C++
//Codechef: mohilllll Codeforces: mohilkhare Google: mohilkhare17
//headers
#include <bits/stdc++.h>
#include <assert.h>
//shorts
#define ll long long int
#define vll vector<long long int>
#define vvll vector<vector<long long int>
#define vpll vector<pair<long long int, long long int>>
#define sll set<long long int>
#define mp make_pair
#define pb push_back
#define endl "\n"
#define fastIO ios_base::sync_with_stdio(false); cin.tie(NULL);
#define MOD 1000000007
//program specific shorts (if any)
using namespace std;
// using namespace std::chrono;
// auto start = high_resolution_clock::now();
// auto stop = high_resolution_clock::now();
// auto duration = duration_cast<microseconds>(stop - start);
// cout << "Time taken by function: " << duration.count() << " microseconds" << endl;
vll solve(map<ll, vll> keeper) {
vll ans;
ll n = keeper.size();
vector<bool> vis(n, false);
for(ll i = 0; i < n; i++) {
if(!vis[i]) {
ll ctr = 0;
vis[i] = true;
stack<ll> wait;
wait.push(i);
while(!wait.empty()) {
ll currNode = wait.top();
wait.pop();
ctr++;
for(auto x : keeper[currNode]) {
if(!vis[x]) {
vis[x] = true;
wait.push(x);
}
}
}
ans.pb(ctr);
}
}
sort(ans.begin(), ans.end());
return ans;
}
int main() {
fastIO;
ll t; cin >> t;
for(ll q = 0; q < t; q++) {
ll n; cin >> n;
map<ll, vll> keeper;
vll vec;
for(ll i = 0; i < n; i++) keeper[i] = vec;
ll k; cin >> k;
for(ll i = 0; i < k; i++) {
ll src, dest; cin >> src >> dest;
keeper[src].pb(dest);
keeper[dest].pb(src);
}
vll ans = solve(keeper);
cout << ans.size() << endl;
for(auto x : ans) cout << x << " "; cout << endl;
}
return 0;
}
Problem: Help the Carpenter
Problem setter: @mohilllll
Logic (Explanation)
Help the Carpenter was a classic coin change with limited coins problem with a trivial implementation of Dynamic Programming. Here, the part which makes this question tricky is that we have a limited supply of coins for each denomination.
We create our DP array dp[K+1][N+1] where K is the number of denominations and N is the target amount. Basically, the only difference between limited bundles and unlimited bundles is that we have to iterate on the number of coins we are using of some particular type such that we ensure we are not violating the constraint i.e. we can use a maximum of D[i] coins for L[i]th type of coin. The base condition is pretty trivial, if you need to have zero logs and you got zero bundles to choose from, your one and the only way to satisfy the requirement is taking zero bundles i.e. doing nothing!
Setter's Solution in Python
from math import ceil
from time import time
# tic = time()
MOD = 1000000007
for t in range(int(input())):
n, k = map(int, input().split())
l = [0] + list(map(int, input().split()))
d = [0] + list(map(int, input().split()))
# dp table (k+1 rows, n+1 cols)
dp = [[0 for i in range(n+1)] for i in range(k+1)]
dp[0][0] = 1
for i in range(1, k+1):
for j in range(n+1):
rem = min(d[i], j//l[i]) # '//' is floor division
for f in range(rem+1):
dp[i][j] = (dp[i][j]%MOD + dp[i-1][j-l[i]*f]%MOD) % MOD
print(dp[k][n]%MOD)
# toc = time()
# Time required in seconds
# print('Time Req:', toc-tic)
Setter's Solution in C++
#include <bits/stdc++.h>
#define ll long long int
#define MOD 1000000007
#define fastIO ios_base::sync_with_stdio(false); cin.tie(NULL);
using namespace std;
using namespace std::chrono;
int main() {
fastIO;
int t; cin >> t;
for(int qq = 0; qq < t; qq++) {
long int n, k;
cin >> n >> k;
long long int l[k+1], d[k+1];
for(long int i = 1; i <= k; i++)
cin >> l[i];
for(long int i = 1; i <= k; i++)
cin >> d[i];
ll dp[k+1][n+1];
memset(dp, 0, sizeof(dp));
dp[0][0] = 1; // if you need to get 0 logs out of 0 types of bundles, only way is to DO NOTHING
for(ll i = 1; i <= k; i++) {
for(ll j = 0; j <= n; j++) {
ll rem = min(d[i], j/l[i]);
for(ll f = 0; f <= rem; f++)
dp[i][j] = (dp[i][j]%MOD + dp[i-1][j-l[i]*f]%MOD) %MOD;
}
}
cout << dp[k][n]%MOD << endl;
}
}
Problem: Power Of Knights
Problem setter: @mishrakeshav
Logic (Explanation)
We can form a directed graph where each knight is a vertex.
Now for any two knights, if ka > kb (given that ka wins against kb),
there is an edge from ‘kb’ to ‘ka’.
Now after forming the graph, let’s consider a case where the ordering
will be impossible.
The ordering will be impossible when
ka > kb > … > ka
Now in this case there cannot be a proper ordering.
This case can be simply detected by checking if there are any cycles in the graph.
If there exists a cycle then ordering is impossible, in this case, print ‘NO’.
If no cycles are detected then we can do topological sorting on the graph.
NOTE: if the ordering is possible then the graph formed will be a special graph called
‘DAG’ (Directed Acyclic Graph).
Refer this link to get a better explanation on how to find cycles in a graph:
Detect Cycle in Directed Graph Algorithm - YouTube
Refer this link to get a better explanation of topological sort:
Topological Sort Algorithm | Graph Theory - YouTube
Since no two knights will have the same power, the answer will always
be unique and there will always be a unique ordering for a valid test case.
Setter's Solution in Python
import math
from collections import deque
class Vertex:
def __init__(self, val):
self.val = val
self.connections = dict()
self.visited = False
self.previous = None
def setVisited(self, visited):
self.visited = visited
def setPrevious(self, val):
self.previous = val
def addConnection(self, node, w=0):
self.connections[node] = w
def isVisited(self):
return self.visited
def getConnections(self):
return self.connections
def __repr__(self):
return str(self.val)
class Graph:
def __init__(self, undirected=True):
self.g = dict()
self.undirected = undirected
self.size = 0
def addVertex(self, val):
self.g[val] = Vertex(val)
def addEdge(self, src, dst, w=0):
if src not in self.g:
self.g[src] = Vertex(src)
if dst not in self.g:
self.g[dst] = Vertex(dst)
self.g[src].addConnection(dst, w)
if self.undirected:
self.g[dst].addConnection(src, w)
def getSize(self):
return len(self.g)
def getVertices(self):
return self.g.keys()
def __contains__(self, val):
return val in self.g
def __iter__(self):
return iter(self.g)
def getVertex(self, val):
return self.g.get(val, None)
def detect_cyles_in_the_graph(g):
def dfs(v, g):
v.setVisited(True)
for node in v.getConnections():
vertex = g.getVertex(node)
if vertex.isVisited():
return True
if dfs(vertex, g):
return True
v.setVisited(False)
return False
for node in g:
vertex = g.getVertex(node)
if dfs(vertex, g):
return True
return False
def topological_sorting(g):
def dfshelper(g, ordering, v):
for node in v.getConnections():
vertex = g.getVertex(node)
if vertex.isVisited():
continue
dfshelper(g, ordering, vertex)
v.setVisited(True)
ordering.appendleft(v.val)
def helper(g, ordering):
for node in g:
vertex = g.getVertex(node)
if vertex.isVisited():
continue
dfshelper(g, ordering, vertex)
ordering = deque()
helper(g, ordering)
return ordering
if __name__ == '__main__':
for t in range(int(input())):
n = int(input())
m = int(input())
g = Graph(undirected=False)
for i in range(m):
a, b = input().split()
g.addEdge(b, a)
if detect_cyles_in_the_graph(g):
print("NO")
else:
print("YES")
order = topological_sorting(g)
for i in order:
print(i)
Setter's Solution in Java
import java.io.*;
import java.util.*;
class Graph {
private int V;
private ArrayList<ArrayList<Integer>> adj;
Graph(int v) {
V = v;
adj = new ArrayList<ArrayList<Integer>>(v);
for (int i = 0; i < v; ++i)
adj.add(new ArrayList<Integer>());
}
boolean isCyclic() {
boolean[] visited = new boolean[V];
boolean[] recStack = new boolean[V];
for (int i = 0; i < V; i++)
if (isCyclicUtil(i, visited, recStack))
return true;
return false;
}
private boolean isCyclicUtil(int i, boolean[] visited, boolean[] recStack) {
if (recStack[i])
return true;
if (visited[i])
return false;
visited[i] = true;
recStack[i] = true;
List<Integer> children = adj.get(i);
for (Integer c : children)
if (isCyclicUtil(c, visited, recStack))
return true;
recStack[i] = false;
return false;
}
void addEdge(int v, int w) {
adj.get(v).add(w);
}
void topologicalSortUtil(int v, boolean visited[], Stack<Integer> stack) {
visited[v] = true;
Integer i;
Iterator<Integer> it = adj.get(v).iterator();
while (it.hasNext()) {
i = it.next();
if (!visited[i])
topologicalSortUtil(i, visited, stack);
}
stack.push(new Integer(v));
}
void topologicalSort() {
Stack<Integer> stack = new Stack<Integer>();
boolean visited[] = new boolean[V];
for (int i = 0; i < V; i++)
visited[i] = false;
for (int i = 0; i < V; i++)
if (visited[i] == false)
topologicalSortUtil(i, visited, stack);
while (stack.empty() == false)
System.out.println("k" + (stack.pop() + 1));
}
}
public class Main {
private static Scanner sc;
public static void main(String args[]) {
sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- > 0) {
int n = sc.nextInt();
Graph g = new Graph(n);
int m = sc.nextInt();
sc.nextLine();
for (int i = 0; i < m; i++) {
String a1 = sc.next();
String a2 = sc.next();
sc.nextLine();
a1 = a1.substring(1);
a2 = a2.substring(1);
int a = Integer.parseInt(a1) - 1;
int b = Integer.parseInt(a2) - 1;
g.addEdge(b, a);
}
if (g.isCyclic())
System.out.println("NO");
else {
System.out.println("YES");
g.topologicalSort();
}
}
// Create a graph given in the above diagram
}
}
Setter's Solution in C++
#include<bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include<cstring>
using namespace __gnu_pbds;
using namespace std;
#define Max 1010
#define ff first
#define ss second
#define ll long long
#define pb push_back
#define ppb pop_back
#define pf push_front
#define ppf pop_front
#define mp make_pair
#define pii pair<ll,ll>
#define vi vector<ll>
#define v vector
#define mii map<ll,ll>
#define pq priority_queue<ll>
#define pqm priority_queue<ll,vi,greater<ll> >
#define setbits(x) __builtin_popcountll(x)
#define zrobits(x) __builtin_ctzll(x)
#define mod 1000000007
#define inf 1e18
#define ps(x,y) fixed<<setprecision(y)<<x
#define mk(arr,n,type) type *arr=new type[n];
#define w(x) ll x; cin>>x; while(x--)
#define all(x) x.begin(),x.end()
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());
typedef tree<ll, null_type, less<ll>, rb_tree_tag, tree_order_statistics_node_update> pbds;
void IO()
{
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
freopen("error.txt", "w", stderr);
#endif
}
void fastIO()
{
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
}
bool topo(v<v<ll>> &a, v<ll> &indeg, v<ll> &ans, ll n)
{
deque<ll> qt;
for (ll i = 1; i <= n; i++)
{
if (indeg[i] == 0)
{
qt.pb(i);
}
}
while (!qt.empty())
{
ll temp = qt.back();
ans.pb(temp);
qt.ppb();
for (ll i : a[temp])
{
indeg[i]--;
if (indeg[i] == 0)
{
qt.pb(i);
}
}
}
return ans.size() == n;
}
int main()
{
fastIO();
// IO();
w(t)
{
ll n, m;
cin >> n >> m;
v<v<ll>> a(n + 1);
v<ll> ans;
v<ll> indeg(n + 1, 0);
for (ll i = 0; i < m; i++)
{
string S1, S2;
cin >> S1 >> S2 ;
ll s1=stoi(S1.substr(1));
ll s2=stoi(S2.substr(1));
a[s2].pb(s1);
indeg[s1]++;
}
if (topo(a, indeg, ans, n))
{
cout << "YES" << endl;
for (ll i : ans)
{
cout << 'k' << i << endl;
}
}
else
{
cout << "NO" << endl;
}
}
return 0;
}
Problem: Many Squares
Problem setter: fallacy69
Logic (Explaination)
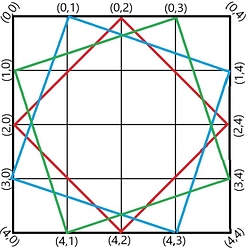
Let’s calculate the area of the 4 squares that are red, blue, green and the black(4 X 4 aligned square)
Length of Blue square’s side: ((4-1)^2+1^2)^\frac{1}{2}= (10)^\frac{1}{2}
Length of Red square’s side : ((4-2)^2+2^2)^\frac{1}{2}=(8)^\frac{1}{2}
Therefore, the sum of the area will be 4^2+(4-1)^2+1^2+(4-2)^2+2^2+(4-3)^2+3^2
Therefore, for an N by N grid, the sum of areas of all the squares formed by using dots that lie on the outline is
N^2+(N-1)^2+1^2+(N-2)^2+2^2... 1^2+(N-1)^2
For an M X N grid, the total number of aligned squares of side length “i” is:
(M-i+1)(N-i+1)
Therefore, the total number of aligned squares will be:
assuming N<M
\sum_i^N (M-i+1)(N-i+1)
Sum of the area formed by an aligned square of length “i” is \frac{2i(i^2+1)}{3}
Therefore, the total area will be for N<M,
\sum_i^N (M-i+1)(N-i+1)\frac{2i(i^2+1)}{3}
using the below formulas, this equation can be simplified
After simplifying we the final equation where N<M:
\frac{-4N^6+6N^5M-18N^5+30N^4M-25N^4+60N^3M+60N^2M+29N^2+24NM+18N}{180}
Note: We use modulus inverse of 180 and use mod at every step
Setter's Solution in Python
MOD = 1000000007
def form(N, M):
n1, m = min(N, M), max(N, M)
n2, n3, n4, n5, n6 = qpow(n1, 2), qpow(
n1, 3), qpow(n1, 4), qpow(n1, 5), qpow(n1, 6)
ans = ((-4*n6 % MOD + 6*n5 % MOD*m % MOD-18*n5 % MOD + 30*n4 % MOD*m % MOD-25*n4 % MOD + 60*n3 % MOD*m %
MOD + 60*n2 % MOD*m % MOD+29*n2 % MOD + 24*n1 % MOD*m % MOD+18*n1 % MOD) % MOD*205555557 % MOD) % MOD
return(ans % MOD)
def qpow(x, n):
if n == 0:
return 1
if n == 1:
return x
v = pow(x, n // 2)
return v * v % MOD * (x if n % 2 == 1 else 1) % MOD
t = int(input())
for i in range(t):
m, n = map(int, input().split())
print(form(m, n))
Setter's Solution in Java
import java.math.*;
import java.util.*;
public class Main {
static BigInteger MOD = new BigInteger("1000000007");
public static void main(String[] args) throws Exception {
// System.setOut(new PrintStream("output.txt"));
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
while (t-- > 0) {
long M = sc.nextLong();
long N = sc.nextLong();
BigInteger n1, n2, n3, n4, n5, n6, m, ans;
n1 = new BigInteger("" + Math.min(M, N));
m = new BigInteger("" + Math.max(M, N));
n2 = n1.modPow(new BigInteger("2"), MOD);
n3 = n1.modPow(new BigInteger("3"), MOD);
n4 = n1.modPow(new BigInteger("4"), MOD);
n5 = n1.modPow(new BigInteger("5"), MOD);
n6 = n1.modPow(new BigInteger("6"), MOD);
// System.out.println(n1+" "+n2+" "+n3+" "+n4+" "+n5+" "+n6+" ");
n6 = n6.multiply(new BigInteger("-4"));
n5 = (n5.multiply(m.multiply(new BigInteger("6")))).add(n5.multiply(new BigInteger("-18")));
n4 = (n4.multiply(m.multiply(new BigInteger("30")))).add(n4.multiply(new BigInteger("-25")));
n3 = (n3.multiply(m.multiply(new BigInteger("60"))));
n2 = (n2.multiply(m.multiply(new BigInteger("60")))).add(n2.multiply(new BigInteger("29")));
n1 = (n1.multiply(m.multiply(new BigInteger("24")))).add(n1.multiply(new BigInteger("18")));
// System.out.println(n1+" "+n2+" "+n3+" "+n4+" "+n5+" "+n6+" ");
ans = n1.add(n2.add(n3.add(n4.add(n5.add(n6)))));
ans = ans.mod(MOD);
ans = ans.multiply(new BigInteger("205555557"));
ans = ans.mod(MOD);
System.out.println(ans);
}
}
}
indent whole code by 4 spaces
Setter's Solution in C++
#include<bits/stdc++.h>
#include<cstdint>
using namespace std;
#define ll long long int
#define MOD 1000000007
void hk()
{
#ifndef ONLINE_JUDGE
freopen("input.txt","r",stdin);
freopen("output1.txt","w",stdout);
#endif
}
ll power(ll x, ll y)
{
ll res = 1;
x = x % MOD;
if (x == 0) return 0;
while (y > 0)
{
if (y & 1)
res = (res*x) % MOD;
y = y>>1;
x = (x*x) % MOD;
}
return res;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
//hk();
ll t;cin>>t;
while(t--)
{
ll a,b,c,d,e,f,g,N,n,M,m,i,j,ans=0;
cin>>N>>M;
m=max(N,M);
a=min(N,M);
b=power(a,2);
c=power(a,3);
d=power(a,4);
e=power(a,5);
f=power(a,6);
ans=((((-4*f%MOD)+MOD)+6*e%MOD*m%MOD-18*e%MOD+MOD+30*d%MOD*m%MOD-25*d%MOD+60*c%MOD*m%MOD+60*b%MOD*m%MOD+29*b%MOD
+24*a%MOD*m%MOD+18*a%MOD)%MOD*205555557%MOD)%MOD;
if(t!=0)
cout<<ans%MOD<<endl;
else
cout<<ans%MOD;
}
return 0;
}
Problem: Mate in Two
Problem setter: @vedant_k07
Logic (Explanation)
First, we need to find the moves a player (Black and White) can play in any given position.
We check the entire board and check for the player’s pieces. Once we have a piece, we try playing all the moves that piece could play.
Eg: if the current player is Black and we find a Pawn, we try to check all the moves that a Black Pawn could play.
Then we try to remove all the illegal moves from the list of our moves. A move is considered illegal if, the player gets a check after playing that move.
A position is considered checkmate if the opponents King is under check and the opponent has no move to play.
The answer is YES if White has a move, for which all the moves that Black could play after that, White will always have move to Mate Black in the second move.
Assuming that at an average a player can play up to 20 different moves, we check for around 20 X 20 X 20 X 20 moves, where to find a move we transverse the entire 8 X 8 board.
The 16 pieces make 8 moves at an average
Hence, we might make 20 X 20 X 20 X 20 X 64 X 16 X 8 computation in the worst case.
To optimize this, we can:
-
Break from all the loops and print the answer if you find the answer to be YES, i.e.
If White has a move X, for which, any move that Black plays after that, White will always have a move to Mate Black -
Not check further moves of Black if we find a move that can avoid checkmate, i.e.
If for White’s move X, Black has a move Y, after which White does not have n=any move that can checkmate Black, we skip checking for the remaining moves that Black can play after White’s move X (As Y is the best move for Black)
Setter's Solution in Python
#import time
from sys import stdin, stdout
import sys
def get_strL(): return list(map(str, sys.stdin.readline().strip().split()))
def Km(board,x,y,pl):
R=[1,1,1,0,0,-1,-1,-1]
C=[-1,0,1,-1,1,-1,0,1]
move=[]
for i in range(8):
if x+R[i]>=0 and x+R[i]<8 and y+C[i]>=0 and y+C[i]<8:
if board[x+R[i]][y+C[i]]!='--' and board[x+R[i]][y+C[i]][1]==pl :
continue
move.append(str(x)+str(y)+" "+str(x+R[i])+str(y+C[i]))
return move
def Qm(board,x,y,pl):
move=Rm(board,x,y,pl)
move+=Bm(board,x,y,pl)
return move
def Rm(board,x,y,pl):
move=[]
i=1
while i+x<8:
if board[x+i][y]!='--':
if board[x+i][y][1]!=pl:
move.append(str(x)+str(y)+" "+str(x+i)+str(y))
break
if board[x+i][y][1]==pl:
break
move.append(str(x)+str(y)+" "+str(x+i)+str(y))
i+=1
i=1
while x-i>=0:
if board[x-i][y]!='--':
if board[x-i][y][1]!=pl:
move.append(str(x)+str(y)+" "+str(x-i)+str(y))
break
if board[x-i][y][1]==pl:
break
move.append(str(x)+str(y)+" "+str(x-i)+str(y))
i+=1
i=1
while i+y<8:
if board[x][y+i]!='--':
if board[x][y+i][1]!=pl:
move.append(str(x)+str(y)+" "+str(x)+str(y+i))
break
if board[x][y+i][1]== pl:
break
move.append(str(x)+str(y)+" "+str(x)+str(y+i))
i+=1
i=1
while y-i>=0:
if board[x][y-i]!='--':
if board[x][y-i][1]!=pl:
move.append(str(x)+str(y)+" "+str(x)+str(y-i))
break
if board[x][y-i][1]== pl:
break
move.append(str(x)+str(y)+" "+str(x)+str(y-i))
i+=1
return move
def Bm(board,x,y,pl):
move=[]
i=1
while i+x<8 and i+y<8:
if board[x+i][y+i]!='--':
if board[x+i][y+i][1]!=pl:
move.append(str(x)+str(y)+" "+str(x+i)+str(y+i))
break
if board[x+i][y+i][1]==pl:
break
move.append(str(x)+str(y)+" "+str(x+i)+str(y+i))
i+=1
i=1
while x-i>=0 and i+y<8:
if board[x-i][y+i]!='--':
if board[x-i][y+i][1]!=pl:
move.append(str(x)+str(y)+" "+str(x-i)+str(y+i))
break
if board[x-i][y+i][1]==pl:
break
move.append(str(x)+str(y)+" "+str(x-i)+str(y+i))
i+=1
i=1
while i+x<8 and y-i>=0:
if board[x+i][y-i]!='--':
if board[x+i][y-i][1]!=pl:
move.append(str(x)+str(y)+" "+str(x+i)+str(y-i))
break
if board[x+i][y-i][1]==pl:
break
move.append(str(x)+str(y)+" "+str(x+i)+str(y-i))
i+=1
i=1
while x-i>=0 and y-i>=0:
if board[x-i][y-i]!='--':
if board[x-i][y-i][1]!=pl:
move.append(str(x)+str(y)+" "+str(x-i)+str(y-i))
break
if board[x-i][y-i][1]==pl:
break
move.append(str(x)+str(y)+" "+str(x-i)+str(y-i))
i+=1
return move
def Nm(board,x,y,pl):
move=[]
R=[-1,-2,-2,-1,1,2,2,1]
C=[-2,-1,1,2,2,1,-1,-2]
for i in range(8):
if x+R[i]>=0 and x+R[i]<8 and y+C[i]>=0 and y+C[i]<8:
if board[x+R[i]][y+C[i]]!='--' and board[x+R[i]][y+C[i]][1]==pl:
continue
move.append(str(x)+str(y)+" "+str(x+R[i])+str(y+C[i]))
return move
def Pm(board,x,y,pl):
move=[]
if pl=='w':
if board[x-1][y]=='--':
move.append(str(x)+str(y)+" "+str(x-1)+str(y))
if x==6 and board[x-2][y]=='--':
move.append(str(x)+str(y)+" "+str(x-2)+str(y))
if y<7 and board[x-1][y+1]!='--' and board[x-1][y+1][1]=='b':
move.append(str(x)+str(y)+" "+str(x-1)+str(y+1))
if y>0 and board[x-1][y-1]!='--' and board[x-1][y-1][1]=='b':
move.append(str(x)+str(y)+" "+str(x-1)+str(y-1))
if pl=='b':
if board[x+1][y]=='--':
move.append(str(x)+str(y)+" "+str(x+1)+str(y))
if x==1 and board[x+2][y]=='--':
move.append(str(x)+str(y)+" "+str(x+2)+str(y))
if y<7 and board[x+1][y+1]!='--' and board[x+1][y+1][1]=='w':
move.append(str(x)+str(y)+" "+str(x+1)+str(y+1))
if y>0 and board[x+1][y-1]!='--' and board[x+1][y-1][1]=='w':
move.append(str(x)+str(y)+" "+str(x+1)+str(y-1))
return move
def changeboard(board,move):
x1=int(move[0])
y1=int(move[1])
x2=int(move[3])
y2=int(move[4])
B2 = [row[:] for row in board]
B2[x2][y2]=B2[x1][y1]
B2[x1][y1]="--"
return B2
def check(b,x,y,pl):
#rook and queen
i=1
while i+x<8:
if b[i+x][y]!="--":
if b[i+x][y][1]!=pl and (b[i+x][y][0]=='R' or b[i+x][y][0]=='Q'):
return True
break
i+=1
i=1
while x-i>=0:
if b[x-i][y]!="--":
if b[x-i][y][1]!=pl and (b[x-i][y][0]=='R' or b[x-i][y][0]=='Q'):
return True
break
i+=1
i=1
while y-i>=0:
if b[x][y-i]!="--":
if b[x][y-i][1]!=pl and (b[x][y-i][0]=='R' or b[x][y-i][0]=='Q'):
return True
break
i+=1
i=1
while y+i<8:
if b[x][y+i]!="--":
if b[x][y+i][1]!=pl and (b[x][y+i][0]=='R' or b[x][y+i][0]=='Q'):
return True
break
i+=1
#Bishop and queen
i=1
while i+x<8 and i+y<8:
if b[i+x][y+i]!="--":
if b[i+x][y+i][1]!=pl and (b[i+x][y+i][0]=='B' or b[i+x][y+i][0]=='Q'):
return True
break
i+=1
i=1
while x-i>=0 and y+i<8:
if b[x-i][y+i]!="--":
if b[x-i][y+i][1]!=pl and (b[x-i][y+i][0]=='B' or b[x-i][y+i][0]=='Q'):
return True
break
i+=1
i=1
while y-i>=0 and x-i>=0:
if b[x-i][y-i]!="--":
if b[x-i][y-i][1]!=pl and (b[x-i][y-i][0]=='B' or b[x-i][y-i][0]=='Q'):
return True
break
i+=1
i=1
while x+i<8 and y-i>=0:
if b[x+i][y-i]!="--":
if b[x+i][y-i][1]!=pl and (b[x+i][y-i][0]=='B' or b[x+i][y-i][0]=='Q'):
return True
break
i+=1
#Knight
R=[-1,-2,-2,-1,1,2,2,1]
C=[-2,-1,1,2,2,1,-1,-2]
for i in range(8):
if x+R[i]>=0 and x+R[i]<8 and y+C[i]>=0 and y+C[i]<8:
if b[x+R[i]][y+C[i]]!='--' and b[x+R[i]][y+C[i]][0]=="N" and b[x+R[i]][y+C[i]][1]!=pl:
return True
#Pawn
if pl=='w':
if y>0 and b[x-1][y-1]=='Pb':
return True
if y<7 and b[x-1][y+1]=="Pb":
return True
else:
if y>0 and b[x+1][y-1]=="Pw":
return True
if y<7 and b[x+1][y+1]=="Pw":
return True
#King
R=[1,1,1,0,0,-1,-1,-1]
C=[-1,0,1,-1,1,-1,0,1]
move=[]
for i in range(8):
if x+R[i]>=0 and x+R[i]<8 and y+C[i]>=0 and y+C[i]<8:
if board[x+R[i]][y+C[i]]!='--' and b[x+R[i]][y+C[i]][0]=="K" and b[x+R[i]][y+C[i]][1]!=pl:
return True
return False
def findking(board,pl):
px=-1
py=-1
out=0
for i in range(8):
for j in range(8):
if board[i][j][0]=="K" and board[i][j][1]==pl:
px=i
py=j
out=1
break
if out==1:
break
return px,py
def moves(pl,board):
move=[]
px,py=findking(board,pl)
fl=0
if board[7][0]=="Rw":
fl=1
for i in range(8):
for j in range(8):
if board[i][j]!='--' and board[i][j][1]==pl:
if board[i][j][0]=="K":
m=Km(board,px,py,pl)
x=0
while x<len(m):
b2=changeboard(board,m[x])
if check(b2,int(m[x][3]),int(m[x][4]),pl):
del m[x]
x-=1
x+=1
move+=m
if board[i][j][0]=="Q":
m=Qm(board,i,j,pl)
x=0
while x<len(m):
b2=changeboard(board,m[x])
if check(b2,px,py,pl):
del m[x]
x-=1
x+=1
move+=m
if board[i][j][0]=="R":
m=Rm(board,i,j,pl)
x=0
while x<len(m):
b2=changeboard(board,m[x])
if check(b2,px,py,pl):
del m[x]
x-=1
x+=1
move+=m
if board[i][j][0]=="B":
m=Bm(board,i,j,pl)
x=0
while x<len(m):
b2=changeboard(board,m[x])
if check(b2,px,py,pl):
del m[x]
x-=1
x+=1
move+=m
if board[i][j][0]=="N":
m=Nm(board,i,j,pl)
x=0
while x<len(m):
b2=changeboard(board,m[x])
if check(b2,px,py,pl):
del m[x]
x-=1
x+=1
move+=m
if board[i][j][0]=="P":
m=Pm(board,i,j,pl)
x=0
while x<len(m):
b2=changeboard(board,m[x])
if check(b2,px,py,pl):
del m[x]
x-=1
x+=1
move+=m
return move
T=int(stdin.readline() )
for t in range(T):
board=[]
for i in range(8):
board.append(get_strL())
#start_time = time.time()
cm=False
move1=moves("w",board)
#print(move1)
for i in move1:
mate2=True
board2=changeboard(board,i)
move2=moves("b",board2)
#print(move2)
for j in move2:
mate1=False
board3=changeboard(board2,j)
move3=moves("w",board3)
for k in move3:
board4=changeboard(board3,k)
move4=moves("b",board4)
if len(move4)==0:
x,y=findking(board4,"b")
if check(board4,x,y,"b"):
mate1=True
if not mate1:
mate2=False
break
if mate2:
cm=True
if cm:
print("YES")
else:
print("NO")
#print("--- %s seconds ---" % (time.time() - start_time))
Congratulations to the Contest Winner!
Please share your valuable Feedback, about the Contest.