PROBLEM LINK:
Author: Shahjalal Shohag
Tester: Ildar Gainullin
Editorialist: Rajarshi Basu
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Constructive, Adhoc
PROBLEM:
You are given two integers N and M. You have to construct a matrix with N rows and M columns. Consider a multiset S which contains N + M integers: for each row and each column of this matrix, the MEX of the elements of this row/column belongs to S. Then, in the matrix you construct, the MEX of S must be maximum possible.
Constraints
- 1 \le T \le 400
- 1 \le N, M \le 100
- the sum of N \cdot M over all test cases does not exceed 10^5
EXPLANATION:
WLOG assume that n\leq m. We need to make the mex of the rows and columns from 0 to K, so that the mex of S can be K+1. We want to maximise this value of K. Obviously, K can be at most N+M. Let’s dive a bit deeper into the actual construction.
In the i^{th} column, let’s try to make the mex =i. Then, we can use the numbers 0,1,2, \dots N, and exclude the number i. But we cannot make the mex greater than N using only columns. Let’s see how such a construction till might look like:
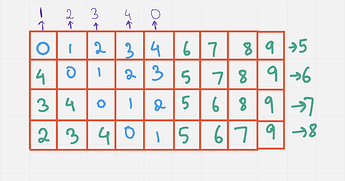
Now lets try to fill in the rows so that we get some new Mex values. The following construction seems natural:
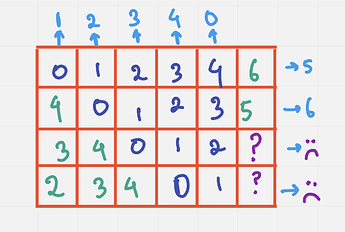
In these examples, n = 4 and m = 9. Now let’s look at a similar construction but with n=4, m = 6 :
Here, whatever you place in the ? places, you wont get a mex greater than 6.
These examples lead to a simple formula : our best possible scenario is min(m,2*n) + 1. The construction method should also be clear from the diagrams. Some intuition might be that,
- by filling columns, we can get upto n values in |S|,
- the number of more values we can get by filling rows is min(m-n,n), that is, either we run out of rows (corresponding to n inside the min), or we run out of columns to make values higher than m (corresponding to m-n inside the min since we have already formed m by filling in columns).
SOLUTION:
Setter’s Code
#include<bits/stdc++.h>
using namespace std;
int MEX(set<int> &se) {
int ans = 0;
while (se.find(ans) != se.end()) ans++;
return ans;
}
int yo(vector<vector<int>> &a) {
set<int> se;
int n = a.size(), m = a[0].size();
for (int i = 0; i < n; i++) {
set<int> cur;
for (int j = 0; j < m; j++) {
cur.insert(a[i][j]);
}
se.insert(MEX(cur));
}
for (int j = 0; j < m; j++) {
set<int> cur;
for (int i = 0; i < n; i++) {
cur.insert(a[i][j]);
}
se.insert(MEX(cur));
}
return MEX(se);
}
int32_t main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
int t; cin >> t;
assert(1 <= t && t <= 400);
int sum = 0;
while (t--) {
int n, m; cin >> n >> m;
assert(1 <= n && n <= 100);
assert(1 <= m && m <= 100);
sum += n * m;
bool f = 0;
if (n > m) {
swap(n, m);
f = 1;
}
int mx = 0;
while (1) {
if (mx <= n);
else if (mx - n <= n && mx <= m);
else break;
mx++;
}
if (n == 1 && m == 1) mx = 1;
vector<vector<int>> a(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
a[i][j] = (j - i + m) % m;
}
}
for (int i = 0, j = n + 1; i < n && j < m; i++, j++) a[i][(j + i) % m] = 0;
if (n == m) {
for (int j = 0; j < m; j++) a[0][j] = n + 1;
}
if (n == 1) {
for (int j = 0; j < m; j++) a[0][j] = !j;
}
if (f) {
vector<vector<int>> b(m, vector<int>(n, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
b[j][i] = a[i][j];
}
}
swap(n, m);
a = b;
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << a[i][j] << ' ';
}
cout << '\n';
}
assert(mx == yo(a));
}
assert(1 <= sum && sum <= 100000);
return 0;
}
Tester’s Code
#include <cmath>
#include <functional>
#include <fstream>
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <set>
#include <map>
#include <list>
#include <time.h>
#include <math.h>
#include <random>
#include <deque>
#include <queue>
#include <cassert>
#include <unordered_map>
#include <unordered_set>
#include <iomanip>
#include <bitset>
#include <sstream>
#include <chrono>
#include <cstring>
using namespace std;
typedef long long ll;
#ifdef iq
mt19937 rnd(228);
#else
mt19937 rnd(chrono::high_resolution_clock::now().time_since_epoch().count());
#endif
int main() {
#ifdef iq
freopen("a.in", "r", stdin);
#endif
ios::sync_with_stdio(0);
cin.tie(0);
auto solve = [&] (int n, int m) {
vector <vector <int> > b(n, vector <int> (m, 1));
if (n == 1 && m == 1) return b;
bool sw = false;
if (n > m) swap(n, m), sw = true;
int ans = n + min(m - n, n) + 1;
vector <vector <int> > a(n, vector <int> (m));
for (int i = 0; i < n; i++) {
int x = (m - i) % m;
for (int j = 0; j < m; j++) {
a[i][j] = x;
x++;
x %= m;
}
}
for (int i = 0; i < n && n + 1 + i < m; i++) {
a[i][(n + 1 + 2 * i) % m] = 0;
}
if (n == m) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
a[i][j] = ((i + j) % n);
}
}
for (int i = 0; i < n; i++) a[0][i] = n + 1;
}
if (!sw) {
return a;
} else {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
b[i][j] = a[j][i];
}
}
return b;
}
};
auto cost = [&] (vector <vector <int> > s) {
int n = (int) s.size(), m = (int) s[0].size();
set <int> arr;
for (int i = 0; i < n; i++) {
set <int> q;
for (int j = 0; j < m; j++) {
q.insert(s[i][j]);
}
int y = 0;
while (q.count(y)) y++;
arr.insert(y);
}
for (int j = 0; j < m; j++) {
set <int> q;
for (int i = 0; i < n; i++) {
q.insert(s[i][j]);
}
int y = 0;
while (q.count(y)) y++;
arr.insert(y);
}
int z = 0;
while (arr.count(z)) z++;
return z;
};
/*
while (true) {
int n = rnd() % 100 + 1;
int m = rnd() % 100 + 1;
auto x = solve(n, m);
if (cost(x) != min(min(n, m) * 2, max(n, m)) + 1 && (n != 1 || m != 1)) {
cout << n << ' ' << m << endl;
cout << cost(x) << endl;
return 0;
}
// assert(cost(x) == min(min(n, m) * 2, max(n, m)) + 1);
}
*/
int t;
cin >> t;
while (t--) {
int n, m;
cin >> n >> m;
auto x = solve(n, m);
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << x[i][j] << ' ';
}
cout << '\n';
}
}
}