PROBLEM LINK -
Author - Sundar Annamalai
Tester - Praveen Dhinwa
Editorialist - Vivek Gupta
DIFFICULTY –
Medium
PREREQUISITES –
PROBLEM IN SHORT -
Given a tree of size N rooted at 1 and M lists of integers. A_i denotes i_{th} list. Consider a bipartite graph G, having M nodes in left bi-partition(denoted by ‘L’) and N nodes in right one(denoted by ‘R’). There is an edge from L_i to all R_{descendants(j)} if A_i contains j. Find the maximum matching in the graph.
QUICK EXPLANATION –
We will construct a flow network. We will add an edge from source to each L_i (left bi-partition, contains M nodes), each of capacity one. We will add an edge from L_i to R_j, each of capacity one, if A_i contains R_j as its element. From each R_j, we will add an edge to R_{child(j)} with the capacity of AT LEAST size of subtree of child(j). We add an edge from each R_j to sink of capacity one. Max-flow of this network is our required answer.
EXPLANATION –
I will use ‘L’ for denoting left bi-partition, containing M nodes and ‘R’ for denoting right partition, containing N nodes.
Let us start with the most naive way of solving this problem which is, to actually construct the graph G, and find the size of maximum matching in that graph using Max-flow algorithm. This reduces to a classic problem and can be done easily. The Bipartite graph G can be constructed by adding an edge from L_i to all R_{descendants(j)} (including R_j) of capacity one, where A_i contains j.
TIME COMPLEXITY –
O(M * N) – For adding edges
O(M*N * Maxflow) – For running Max-flow algorithm, where maxflow can be at most N.
Since our Max-flow algorithm can’t run in time limit, we need to reduce the number of edges in our graph.
KEY OBSERVATIONS –
1. If there is an edge from L_i to some R_j, we will also have an edge from L_i to R_k, where k is any descendant of j.
2. It doesn’t matter from where the flow occurs, direct or indirect. This means that if we add some edges and modify the path of flow to go via those nodes/edges, instead of the initial one, the amount of flow would still remain the same. Look these images below for understanding.
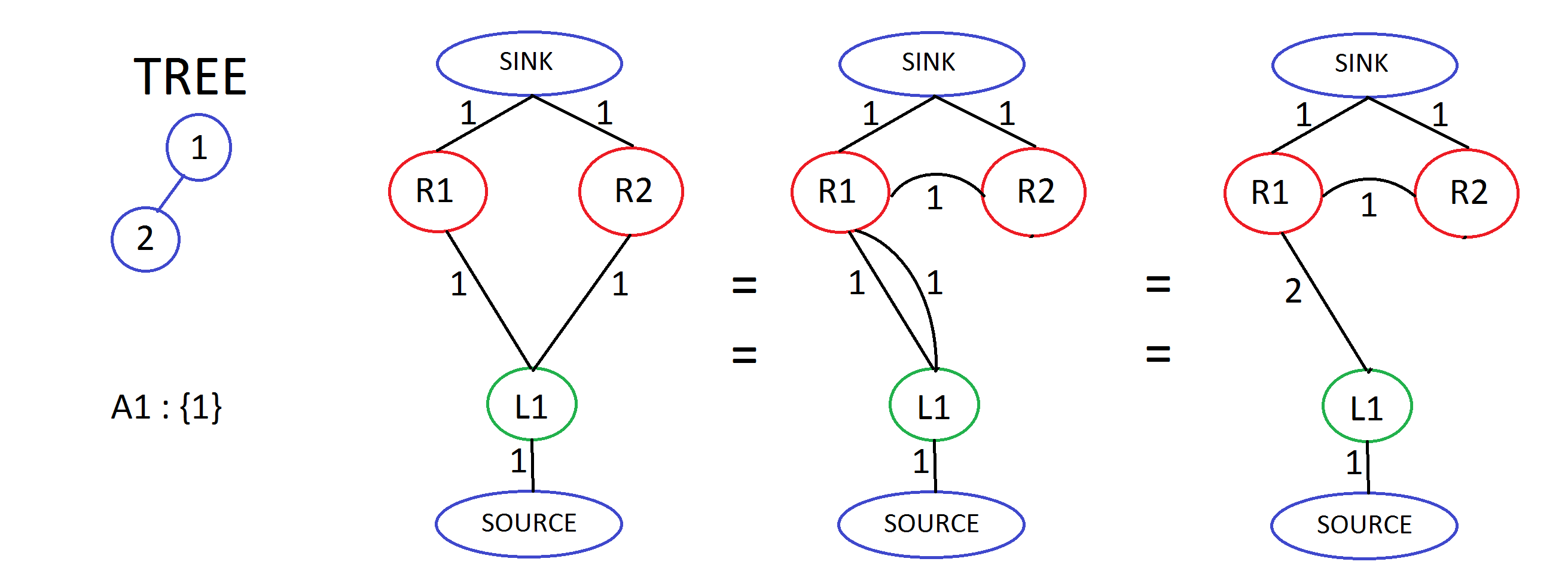
A more explained example -

INTENDED SOLUTION –
With the help of above observations, we can say that instead of adding edges from each L_i to all R_{descendants(j)}, where A_i contains j, we will now add edge from L_i to only elements of A_i and from each R_j to all R_k, where k is a descendant of j. All edges are of capacity one.
This doesn’t help the time complexity, but the problem can be reduced from this stage.
Now, we again apply second observation to say that instead of direct flow from each R_j to all R_k, where k is a descendant of j, we make the path of flow from j to k, go via all the R_p, where p is a node which lies between the path from j to k in the tree. p can be defined as child of j and ancestor of k in the tree. When we do this, we will have size-of-subtree(p) number of edges from R_{parent(p)} to R_p. This is equivalent to a single edge from R_{parent(p)} to R_p of capacity of size of subtree of p. Replacing p by j, all we need to do is only add edges from each R_{parent(j)} to R_j with the capacity of size of subtree of j and run the max-flow algorithm.
Another way to look upon this is to use observation 1 and say that if there is an edge from R_j to some R_k, R_j will also have an edge to all R_{descendants(k)}, so we can say it is enough to have an edge from all R_{parent(c)} to R_c with the capacity of at least size of subtree of c for some c to keep propagating the flow towards all the descendants. I used the word ‘at least’ because we are already keeping the capacity of the edge such that at least one unit is reaching every descendant, and because every R_j can send only one unit to the sink, it won’t matter if we keep the capacity to be size of subtree or one trillion. So, you don’t have to actually find size of subtree of every node but instead, keep the capacities of the edges greater than size of tree$(N)$.
PROOF OF CORRECTNESS -
We can say that given a matching in our original bipartite graph G, you can get a flow of at least that much in this network. That’s trivial, hence matching <= flow.
And given a flow in our network, we can get a matching related to it in bipartite graph G. In our network, a flow path can be described as - source, L_i, R_j, R_{child(j)}, ... , R_{K^{th} child(j)}, sink. This path of flow will relate to the edge from L_i to R_{K^{th} child(j)} in bipartite graph G. Edges from source to L_i and from R_{K^{th} child(j)} to sink are used and thus, neither of both will be used again and each flow path corresponds to a unique edge between a unique L_i and a unique R_j in a matching.
Thus, flow <= matching \implies flow = matching. Max-flow of this network will give maximum number of unique pairs and hence maximum matching in the bipartite graph G. K can be zero also, in that case, it refers to itself. Each node is 0^{th} child of itself.
TIME COMPLEXITY –
Number of edges -
Max-flow can be at most N = 5000
Time complexity of Max-flow algorithm = O(Edges * Maxflow) = O(1.25 * 10^8) per query.
4 queries should work in given time limit of 3.5 seconds.
SECOND APPROACH -
In this solution, instead of adding edge from R_{parent(j)} to R_j with the capacity of at least subtree(j), we will add edge from R_j to R_{parent(j)} with the capacity of ‘exactly’ size of subtree(j) and add only one edge from R_1 to the sink of capacity N. No need to add edges from other R_j to sink. This works because, we just changed and re-directed the flow from every R_j to go via R_1 and added a single edge of capacity N to the sink to account for the re-direction of flow. This is again, through observation 2.
This time, I used the word ‘exactly’ because, the edge from R_1 to sink is no longer of capacity one, and having more capacity can cause more flow and distort the answer.
TIME COMPLEXITY -
Second approach has a slightly higher time complexity by a constant factor than first one because the flow to sink can happen only from one node. Also, the edges have a limited capacity. All this increases the length of augmenting path and hence the time of DFS part in max-flow algorithm. No major change as such.
IMPLEMENTATION -
Editorialist’s code for first approach - here.
Editorialist’s code for second approach - here.
Setter’s code using second approach - here.
Tester’s code using second approach - here.
NOTE -
This link has an excellent figure with a short explanation of the first approach for better understanding - here.