PROBLEM LINK:
Editorialist: Soumik Sarkar
DIFFICULTY:
HARD
PREREQUISITES:
Basic maths
PROBLEM:
There are n_m men and n_h horses. The speed of each man is v_m and speed of each horse is v_h. The men must cover a straight distance d. The men may utilize the horses. A horse can carry at most one man at a time and can obey instructions even when riderless. No time is needed in mounting or dismounting from a horse or reversing the direction of motion. What is the minimum time the men need to cross the distance?
EXPLANATION:
The difficult thing is to discover the optimal approach. Once the approach is known, a little bit of algebra will give the answer. There also also two trivial cases. When v_m \ge v_h, the men will be faster without horses and will take time d/v_m. When n_h \ge n_m every man gets a horse and reaches destination in d/v_h time. Now to the main problem
Simpler case with v_m = 0
Consider a case where the men cannot move and must rely on the horses. Although such a test case does not exist due to the constraints, solving this will help in finding the general solution. The solution is as follows.
The distance d is divided into n_h ranges. Each horse h_i is given the i^{th} range. First all horses start out carrying a man. Each horse carries his man to the end of his assigned range and drops him off. Then he returns to the beginning of his range and picks one man up. He repeats moving back and forth across his range until he picks up the last man. Then he moves to the destination.
As an example, consider n_h = 2 and n_m = 3. The time it takes for a horse to move across one range is t. Below are the states after every t time.
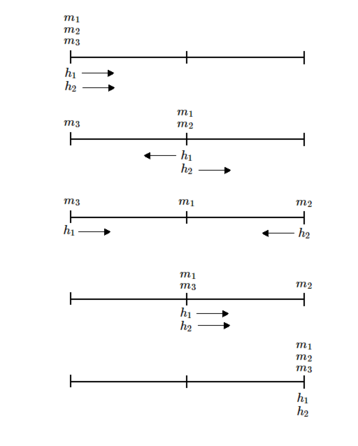
The general case
The previous solution needs to be modified to be applied to the general case. All men now move at v_m forward when they are not on a horse. What difference does that make?
- When a horse is on his way back across his range after dropping off a man, he will meet the next man before he reaches the beginning of the range.
- If the last horse drops off men at the destination, that’s a waste of time since one man will reach before the other. Instead, it is better to drop off the man at some distance from the destination in such a way that in the end all men and horses reach together.
It is extremely helpful to the draw the displacement-time graph of the scenario.
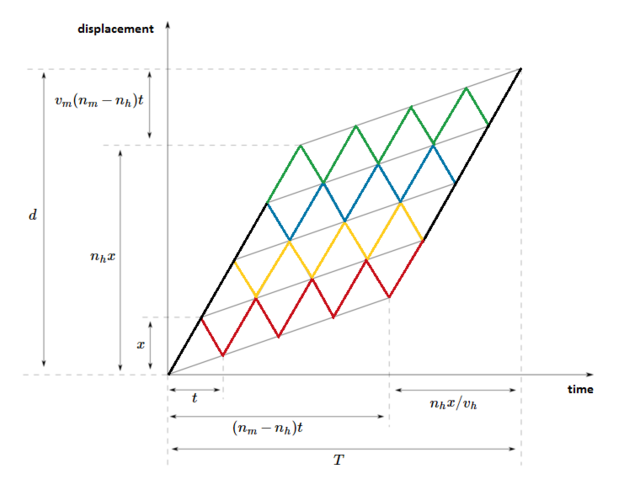
The steeper lines are the trails of the horses with slope v_h or -v_h, and the gentler lines those of the men with slope v_m. The red, yellow, blue and green trails belong to different horses. The black lines indicate where more than one horse travel in parallel. Each horse moves back and forth and carries one man across his range each time. At points where two horses meet they can easily swap their ranges, but the overall effect remains the same.
We do not know beforehand what range should be assigned to each horse, so let it be x. Also let the time taken for a horse to move across his range and then partly back until he meets a man be t. Then we can calculate t as
Next consider the first man dropped off at distance n_hx by the last horse. From there he moves at v_m until he reaches d. Now the horse goes back and comes with another man again and again, until at the end all n_h horses bring n_h men. Since the total men is n_m, the number of times he sees the horse go and come back is n_m - n_h.
We can plug in the expression for t, and simplify to get
From the graph we can see the total time taken T is
Complexity is \mathcal{O}(1).
It is convenient to use Python here since it has built-in support for fractions. Using Java or C++ it is necessary to manually implement operations on fractions.
ALTERNATIVE SOLUTION:
If you have an alternate strategy that also takes minimum time, feel free to share it below.
EDITORIALIST’S SOLUTION:
Editorialist’s solution can be found here.