PROBLEM LINK:
Author: Praveen Dhinwa
Tester: Hanlin Ren
Editorialist: Hanlin Ren
DIFFICULTY:
SIMPLE
PREREQUISITES:
None
PROBLEM:
Given a string s[1\sim n], does there exist a permutation p of 1,2,\dots,n such that, if we let t[i]=s[p[i]], then t is palindrome?
EXPLANATION:
This problem is equivalent to: can we rearrange the characters of s into a permutation?
Let’s count the number of occurrences of every characters in a-z. For a char c, let cnt[c] be the number of times c occur in s.
If there are two chars c_1,c_2(c_1\ne c_2) such that both cnt[c_1] and cnt[c_2] is odd, then the answer is no.
- To see this, consider any palindromic string t and any char c. Suppose t[i]=c.
- If the length n of t is even, then t[n-i+1]=c. Since n is even, n-i+1 and i has different parity and hence i\ne n-i+1. Also n-(n-i+1)+1=i, so we say i and n-i+1 is a pair. Any pair must use the same character, so any character must occur an even number of times.
- If the length n of t is odd, the above argument holds, too, except that the central char(t[\frac{n+1}{2}]) is matched with itself. In this case, this char appears an odd number of times, and is the only char that appears an odd number of times.
- See figure below. n=7, pairs are (1,7),(2,6),(3,5), and t[4] is matched with itself, and hence appears an odd number of times.
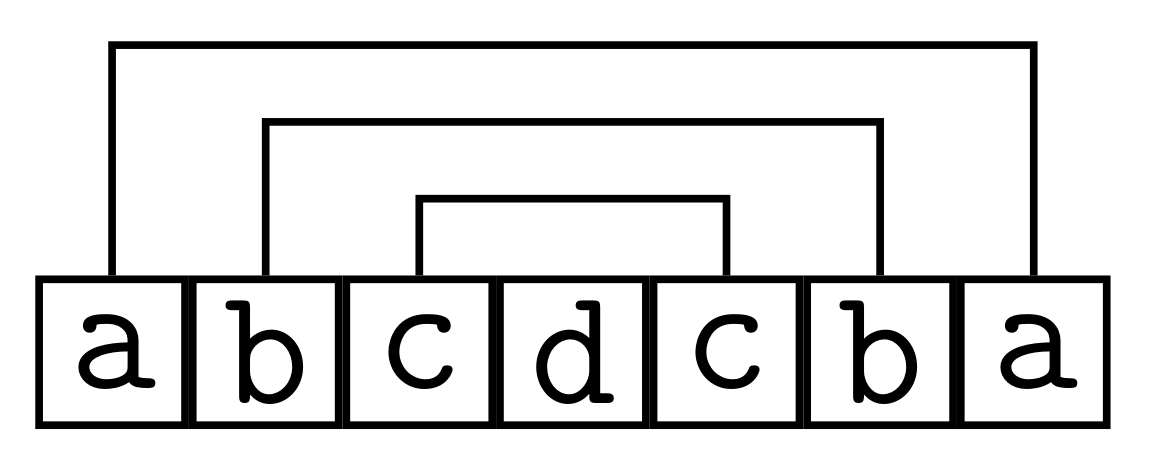
- In conclusion, if C is the number of chars c that cnt[c] is odd, and s can be arranged into a palindrome, then C\le 1.
The converse is also true: if there are at most 1 characters c with cnt[c] odd, then the answer is yes. Here is one of the constructions.
- Let’s construct the permutation char-by-char. Let c iterate from
atoz.- If cnt[c] is odd, we ignore c(that is, we consider c later). At most one such c exists.
- We maintain two pointers l and r. Initially l=0,r=n+1. The permutation p[1\sim l] and p[r\sim n] is already filled.
- We scan s. Each time we meet a c, say t[i]=c,
- if this is the 1,3,5,\dots,(odd) time we meet c, we assign it to the left: l\gets l+1 and p[l]\gets i;
- otherwise (this is the 2,4,6,\dots time we meet c), we assign it to the right: r\gets r-1 and p[r]\gets i.
- The picture below shows how we fill p when s=
abdacbabdccba, i=b.
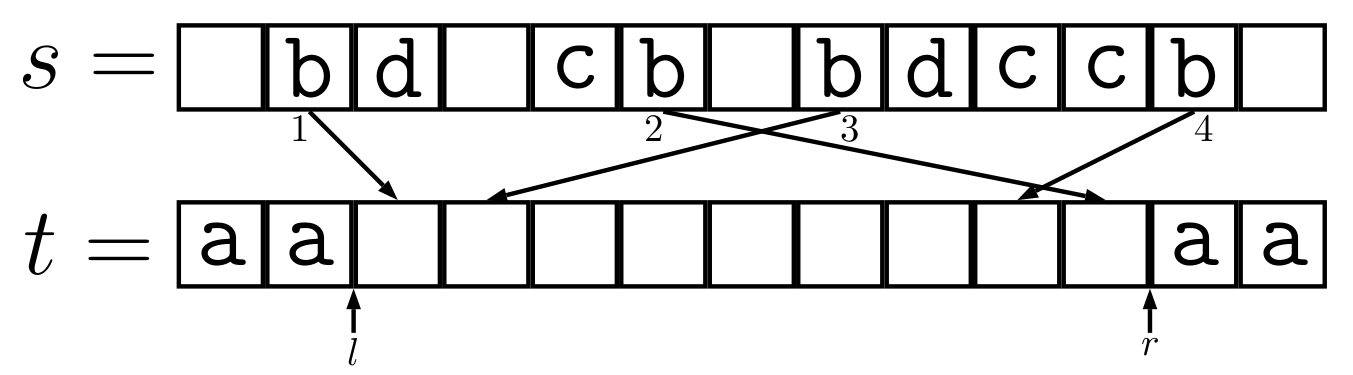
- At last, in case that n is odd, we need to deal with the c where cnt[c] is odd. That’s easy: p[l+1\sim r-1] is unfilled, and we fill them by char c.
- This is a valid answer. Time complexity: O(\sigma\cdot n). (\sigma=26)
ALTERNATIVE SOLUTIONS
This is a constructive problem. I think there’ll be many solutions. Please feel free to share your solution.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.
