PROBLEM LINK:
Author: Praveen Dhinwa
Tester: Hanlin Ren
Editorialist: Hanlin Ren
DIFFICULTY:
MEDIUM
PREREQUISITES:
Convex Polygon, constructive algorithms
PROBLEM:
Given an n-sided convex polygon where all vertices have integral coordinates. Output \lfloor n/10\rfloor distinct integral points strictly inside the polygon.
QUICK EXPLANATION:
This editorial contains 3 solutions: (Setter’s solution is the easiest among them)
Setter’s solution
- For a polygon of 10 points, one can easily find one point by checking the midpoints of some chords.
- Let P_1,P_2,\dots,P_n be the vertices.
- For each k=10i+1, we find one integral point in the convex hull of P_k,P_{k+1},\dots,P_{k+9}.
A dfs/bfs-based solution
- We need a data structure that given a point, tells in O(\log n) time if the point is strictly in the polygon.
- First, we arbitrarily find one point in the polygon.
- Then we check if its neighbors are in the polygon; check its neighbors’ neighbors; and so on.
Tester’s solution
- Let U(x_0) be the intersection of x=x_0 with the upper hull. Similarly L(x_0) for lower hull.
- Find (roughly) the smallest x_0 such that the open interval (L(x_0), U(x_0)) contains some integer.
- Imagine a vertical line at x=x_0. Then we can output all integral points on the vertical line.
- We repeatedly increase x_0, moving the vertical line rightwards. During this process we can maintain L(x_0),U(x_0) and iterate all integral points in the polygon.
Setter’s Solution
Click to view
A special case
Let’s first consider the case when n=10. Let the points be P_1,P_2,\dots,P_{10} in order. We want to find one integral point strictly inside the polygon. In fact, this can be done by the following: we simply look at every pair (i,j), and check if the midpoint of some P_i,P_j is integral. Of course, only pairs that are not on the edge of the polygon counts. Recall the midpoint of two points (x_1,y_1) and (x_2,y_2) is (\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}).
Does this algorithm guarantee a solution? This can be proved by pigeonhole principle: imagine there are 4 holes: 00, 01, 10, 11. A point (x,y) is a pigeon, and it goes to the hole whose first bit is (x\bmod 2) and second bit is (y\bmod 2), e.g. (3,4) goes to 10 and (5,5) goes to 11. We have P_1,P_3,P_5,P_7,P_9 which are 5 pigeons, so 2 of them must be in the same hole, say P_i and P_j. The midpoint of P_i and P_j must be integral, and (i,j) is not on the edge.
General solution
Things become easy when we solved the n=10 case. Let the points be P_1,P_2,\dots,P_n. For any 0\le k<\lfloor\frac{n}{10}\rfloor, we regard P_{10k+1},P_{10k+2},\dots,P_{10k+9} as a polygon and find a point in it.
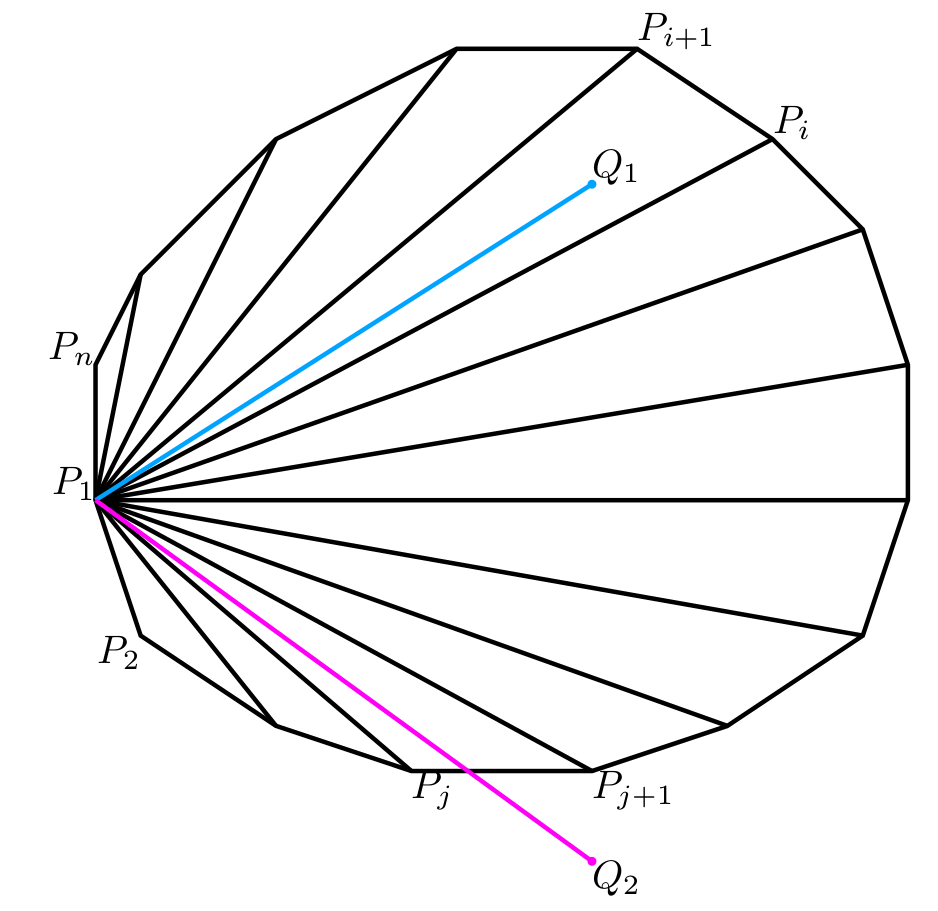
For example, in the polygon below, \lfloor n/10\rfloor=5, so we find a point Q_1 in the convex hull of \{P_1,P_2,\dots,P_{10}\}, find Q_2 in the convex hull of \{P_{11},\dots,P_{20}\}, and so on until Q_5. Then we output \{Q_1,Q_2,\dots,Q_{\lfloor n/10\rfloor}\}. We can guarantee that the points are integral, pairwise distinct, and strictly inside the polygon.
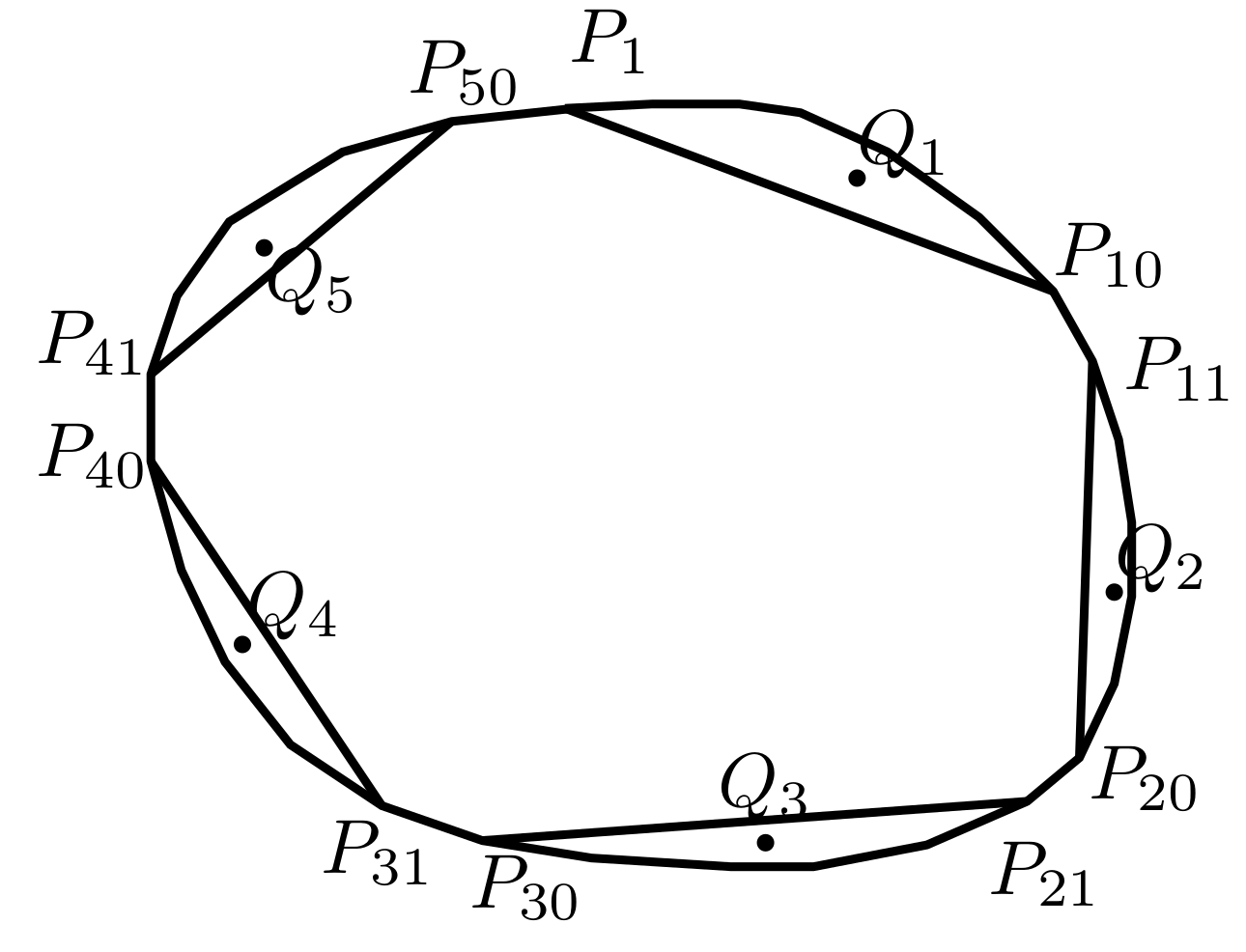
The total time complexity is O(n).
DFS/BFS Based Solution
Click to view
This problem can also be solved by something similar to DFS/BFS. Firstly, we can find an arbitrary point strictly inside the polygon, by what we did in Setter’s solution. (Or by whatever algorithm you like, if it’s correct and fast!) Then we start to search the neighbors of this point, until we find \lfloor n/10\rfloor points. One possible pseudocode is as follows:
dfs(p) //p is a point
if num_visited == n / 10
end the search process
for q in p's neighbors //p has 4 neighbors
if q is strictly inside the polygon
if q is not visited
visited[q] = 1 //we can use set<point> to maintain visited points
num_visited += 1
dfs(q)
//below is main procedure
p = arbitrary point strictly inside the polygon
num_visited = 1
visited[p] = 1
dfs(p)
A data structure
In the above pseudocode, we need a data structure that given a point (x,y), check if (x,y) is strictly inside the polygon. We can do it in O(\log n) time, and actually there are (at least) two simple ways to do it.
Way 1: Finding upper/lower hulls
Click to view
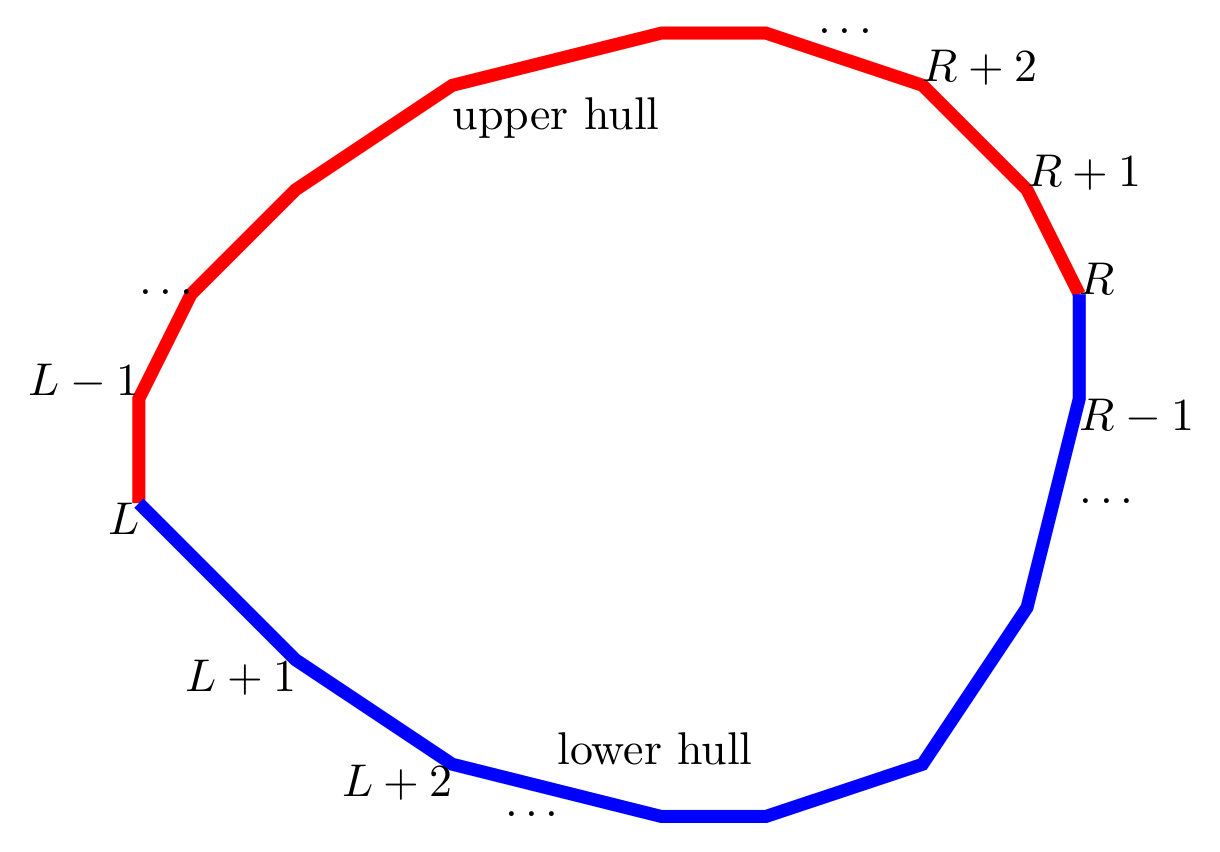
First, let’s find the upper and lower hull. Let L=\arg\min_{i=1}^nx[i], R=\arg\max_{i=1}^nx[i]. Since the polygon is given in counter-clockwise order, the upper hull is given by P_R, P_{R+1}, \dots, P_L and the lower hull is P_L, P_{L+1}, \dots, P_R.
Consider a query point Q=(x_0,y_0). If it’s strictly below the upper hull, and strictly above the lower hull, then it’s inside the polygon; otherwise it’s not. Take the upper hull as an example. By binary search we can find the smallest i s.t. x_i\ge x_0. We find the y coordinate of the intersection of the segment (x_{i+1},x_i) and the vertical line x=x_0. If y>y_0, then Q is strictly below the upper hull. For example, in the following picture, Q_1 is strictly below the upper hull, but Q_2 is not.
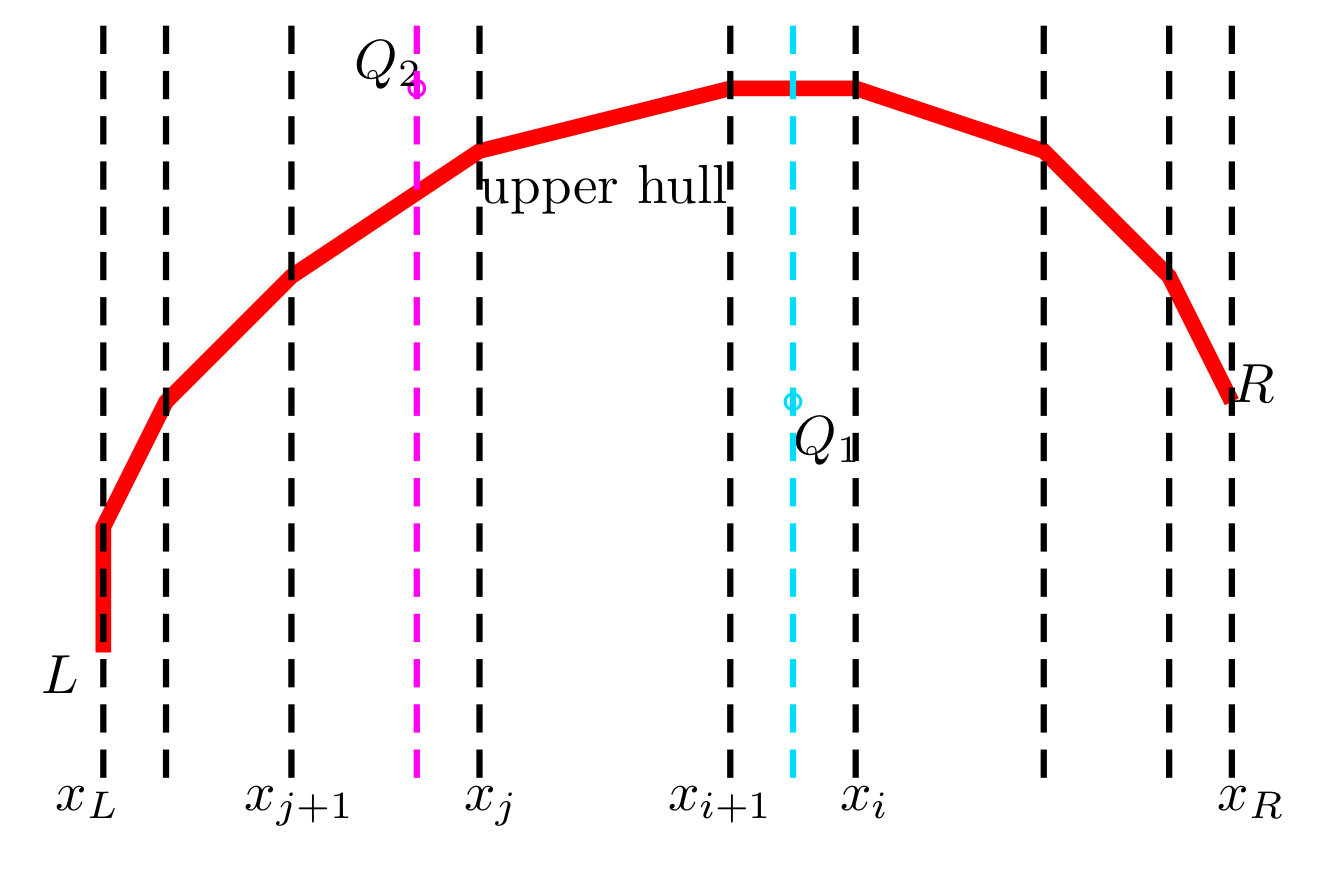
We use the same procedure to check if Q is above the lower hull. Then we can decide whether a point is strictly inside the polygon in two binary searches.
Way 2: Sorting around the leftmost point
Click to view
This method works for any point but we consider the leftmost point for convenience. The leftmost point of a convex polygon is defined as the point with smallest x. In case a tie happens, we arbitrarily choose one. Suppose this polygon is P_1P_2\dots P_n, and the leftmost point is P_1. We define the angle of a point (x,y) is \mathrm{atan2}(y-P_1.y,x-P_1.x)(See atan2). To give a first impression, consider the following figure:
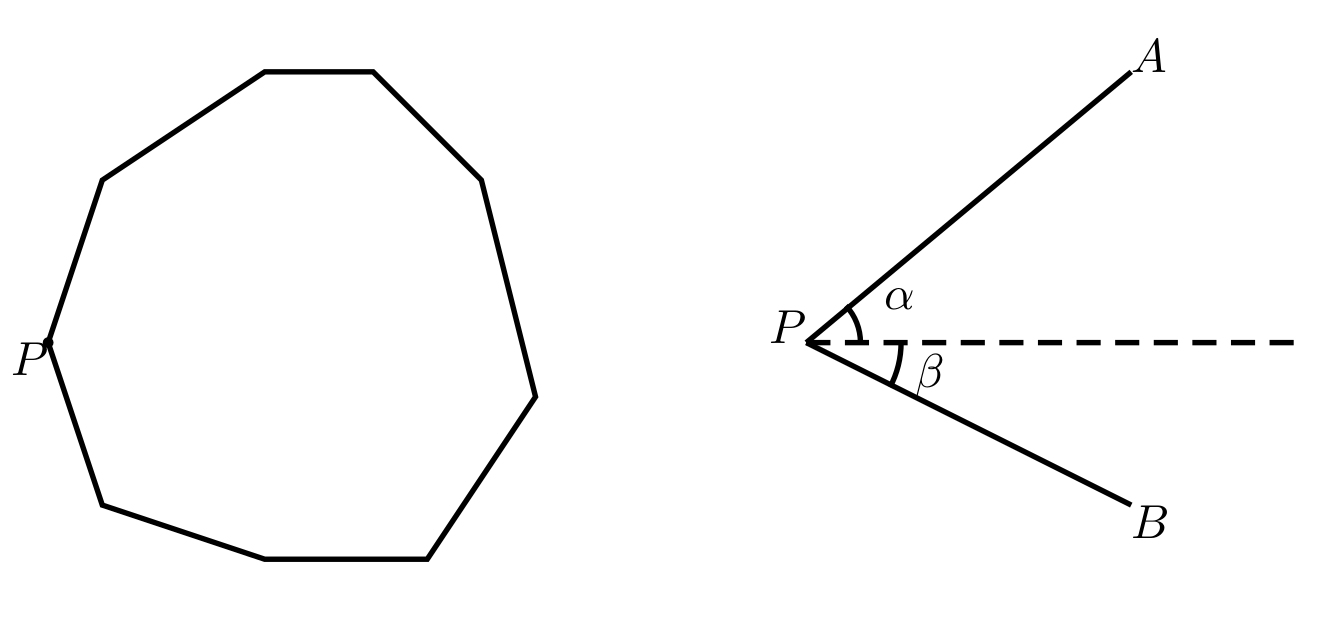
- In the left polygon, the point P is the only lowest point;
- In the right figure, the angle of A is \alpha, while the angle of B is -\beta.
- It’s easy to see that, for any 2\le i\le n, the angle of P_i is in [-\pi/2,\pi/2].
In the preprocessing phase, we just compute the angles of all points \alpha_2,\alpha_3,\dots,\alpha_n. We have \alpha_2<\alpha_3<\dots<\alpha_n.
Consider a query point Q(x,y) whose angle is \alpha. If \alpha\le \alpha_2 or \alpha\ge\alpha_n, it’s definitely not in the polygon(strictly); otherwise we find the largest i such that \alpha_i < \alpha. If the segment (P_1,Q) intersects with (P_i,P_{i+1}), then Q is not in the polygon(see Q_2 of the following figure); otherwise Q is in the polygon. This takes O(\log n) time.
Tester’s Solution
Click to view
- Let’s define L(t) be the y coordinate of the intersection point of the lower hull and vertical line x=t.
- Similarly define U(t) be that of upper hull and vertical line x=t.
- Find the smallest x_0 such that the open interval (L(x_0),U(x_0)) contains integer.
- For all integer y\in (L(x_0),U(x_0)), we output (x_0,y_0). That is, the blue points below.
- Imagine we have a vertical line at x=x_0. Now we move it to the right, i.e. x_0\gets x_0+1.
- In this process, we can maintain L(x_0) and U(x_0) efficiently by maintaining the intersected segment of polygon and vertical line, i.e. the red segments below.
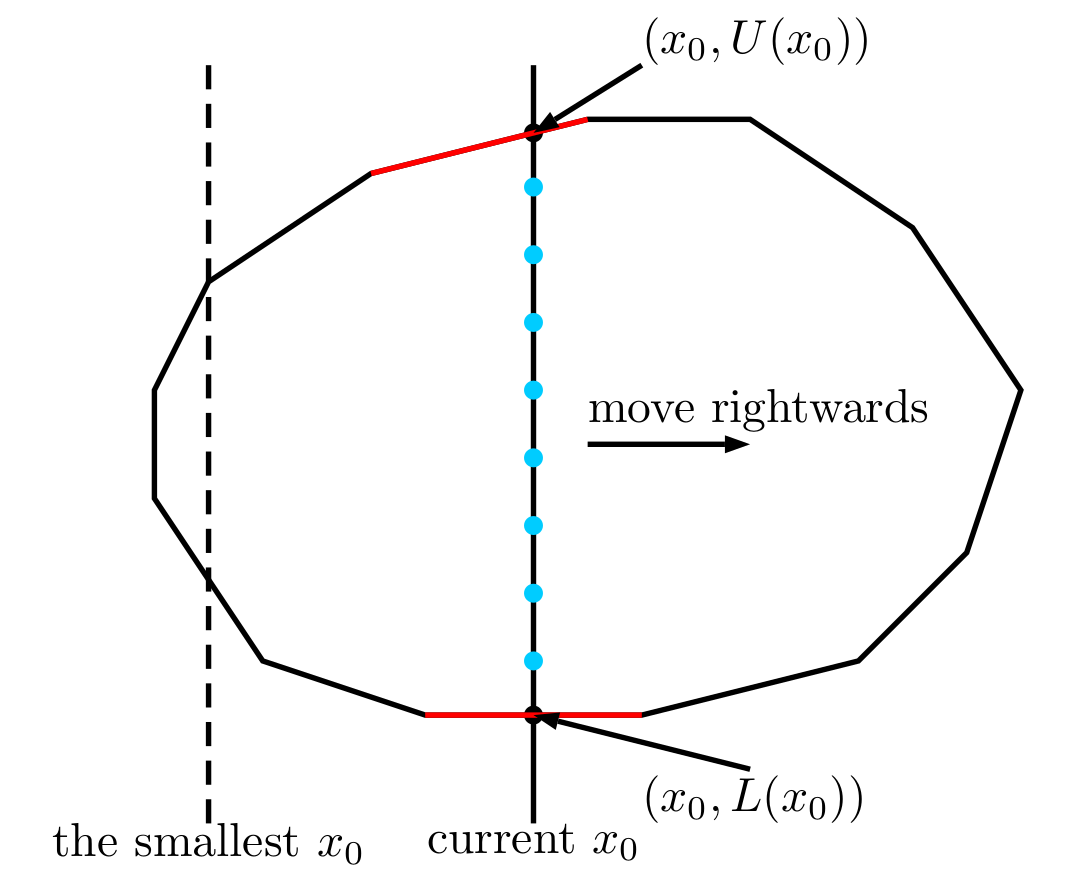
- We repeatedly move the vertical line rightwards, i.e. x_0\gets x_0+1. When we increase x_0, we maintain the two red segments, and L(x_0),U(x_0) can be computed in O(1) time. Then we spend O(U(x_0)-L(x_0)) time to output all integral points on the vertical line. Remember to quit as soon as we have \lfloor n/10\rfloor points.
- The time complexity is O(n).
How to find the first x_0?
We don’t need to find x_0 accurately; an estimate x'\in [x_0-5,x_0] is okay. (In fact this 5 is arbitrary; it means we scan 5 useless points.) Let L be the leftmost point. To find x_0, we consider three cases:
- Case I: y[L+1]\ne y[L] and y[L-1]\ne y[L]. In this case, x_0=x[L]+1.
- Case II: y[L-1]=y[L]. Since L-1,L,L+1 are not collinear, y[L+1]\ne y[L]. Since \cot\theta=\frac{x[L+1]-x[L]}{y[L+1]-y[L]}, the answer is x[L]+\cot\theta=x[L]+\frac{x[L+1]-x[L]}{y[L+1]-y[L]}.
- Case III: y[L+1]=y[L]. This is symmetric to Case II, and the answer is x[L]+\frac{x[L-1]-x[L]}{y[L-1]-y[L]}.

Bonus: how to generate a convex polygon?
Click to view
There is an easy way to generate convex polygons:
- Take n-1 random vectors v_1,v_2,\dots,v_{n-1}, and compute v_n=-\sum_{i=1}^{n-1}v_i. This is to ensure that \sum_{i=1}^nv_i is the zero vector.
- Then sort v_1,v_2,\dots,v_n by their angle(the angle of vector (x,y) is defined as \mathrm{atan2}(y,x), see atan2).
- Let’s walk around the vectors. Choose a start point P, and the vertices of the polygon are P,P+v_1,P+v_1+v_2,P+v_1+v_2+v_3,\dots,P+\sum_{i=1}^{n-1}v_i.
- See the figure below for better understanding.

Basically we use this method to construct test data. We also have some handmade data to hack flawed solutions.
ALTERNATIVE SOLUTION:
There are many solutions for this problem. Please, feel free to share your approaches!
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution 1 can be found here.
Tester’s solution 2 can be found here.
Tester’s solution 3 can be found here.