Problem Link
Author: Tianyi
Tester: Misha Chorniy
Editorialist: Bhuvnesh Jain
Difficulty
HARD
Prerequisites
Flows, Minimum Cut
Problem
You are given a grid consisting of 0(white), 1(black) and ?(unknown). You are required to convert ? to 0 or 1 such that the following cost is maximised:
where B_i denotes the number of ways to select a black square of size i, W_i denotes the number of ways to select a white square of size i and C_{B, i} and C_{W, i} arrays is provided in input.
Explanation
Subtask 1: N * M ≤ 10
A simple brute force which converts each ? to 0 or 1 and calculates the cost of the board is sufficient to pass this subtask. The time complexity of the above approach is O(2^{NM}).
Subtask 2, 3: N * M ≤ 500
The constraints are small and since the problem is related with maximisation, it hints towards either dynamic programming or flows based solution generally. We will use minimum cut to solve this problem. In case you are not familiar with the topic or its usage in the problem, please you through this awesome video tutorial by Anudeep Nekkanti.
Now, using the ideas similar in the video, we design the below algorithm.
-
We iterate through each possible square in the grid. If it only consists of white or black cells, add the required cost depending on size to the answer. If it consists of some question marks as well, then we check if it can be converted to only white cells or black cells or both. We optimistically add the required white/black contribution to the answer. (Note that it is similar to the problem where we add all the possible contribution first to the answer, and in order to maximise the final answer, use the minimum cut algorithm to find the minimum contribution which needs to be taken back from the answer. This is the most important step of the problem.). Let the optimistic answer we calculated now be known as “initial ans”.
-
Now, we construct a graph as follows. Consider a source of a white node and sink of a black node. For every optimistic conversion of a square to white/black you considered (by converting some ? to 0 or 1), add an edge between a new node to the corresponding white (source) or black (sink) node with the weight of the edge as the cost of that square. Also, add edges of weight INFINITY (some large constant) between every cell containing ? to the new node. To get an understanding of the graph construction, see the below diagram showing the graph for the sample case in the problem.
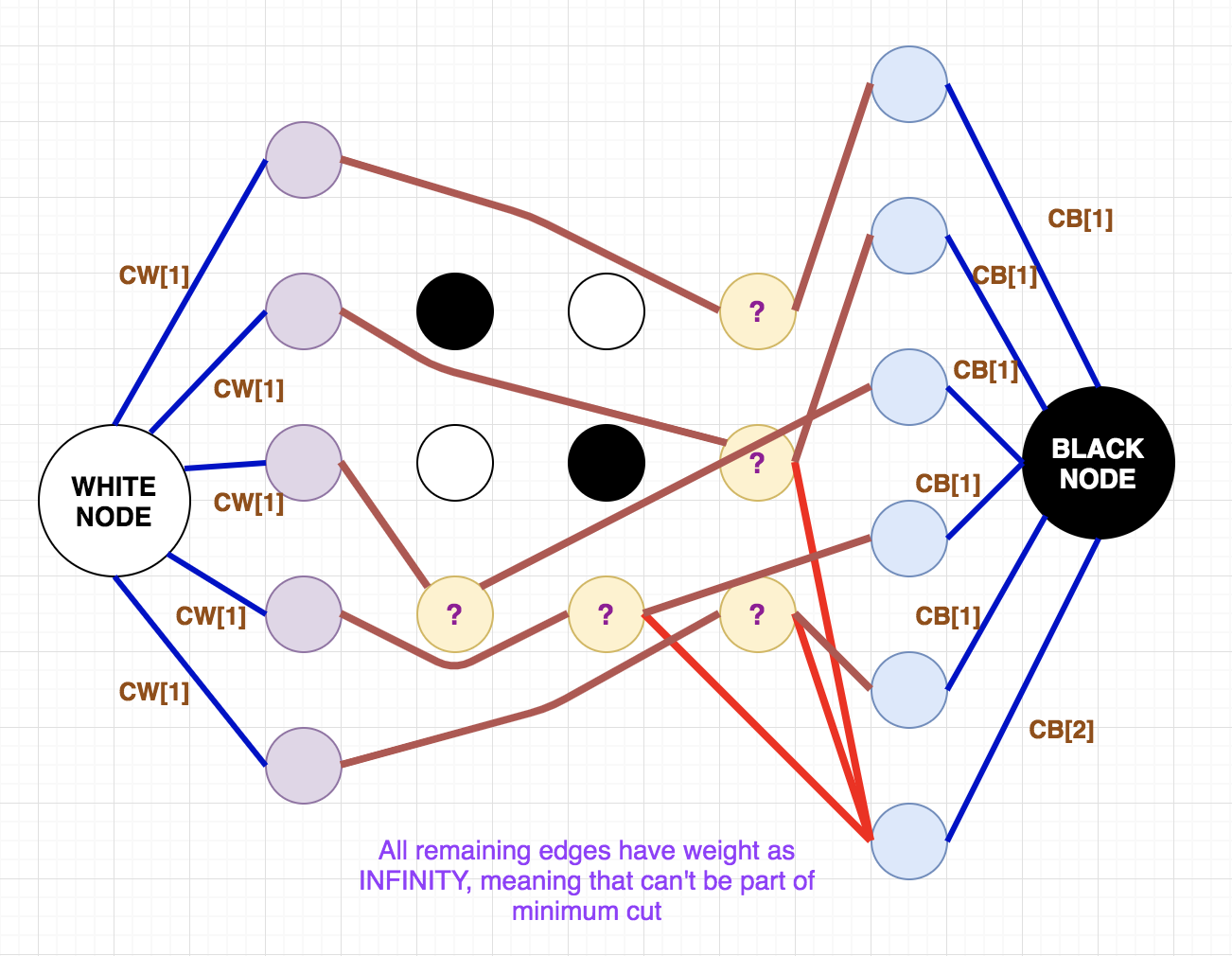
- The answer to the problem is “initial ans - maximum_flow of above graph”.
To understand why the above algorithm works, we will reason cutting of each edge in terms of minimum cuts and the rewards/penalties it provides.
It is sure that edges of weight INFINITY will never be considered in the minimum cut of the graph. So we consider the remaining 2 scenarios.
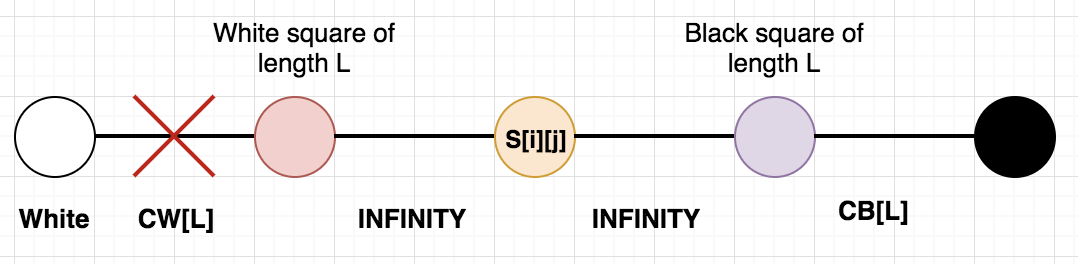
This image shows the scenario where the edge containing white node (source) and the node representing an optimistic white square of length L is cut. This implies one of the ? in the square chose to convert to 1 instead of 0. This can happen for whatever reason, for example - It might to costlier to cut the corresponding black edges to which the ? node also connects (such a node will exist otherwise there will be no path from white i.e. source to black i.e. sink).
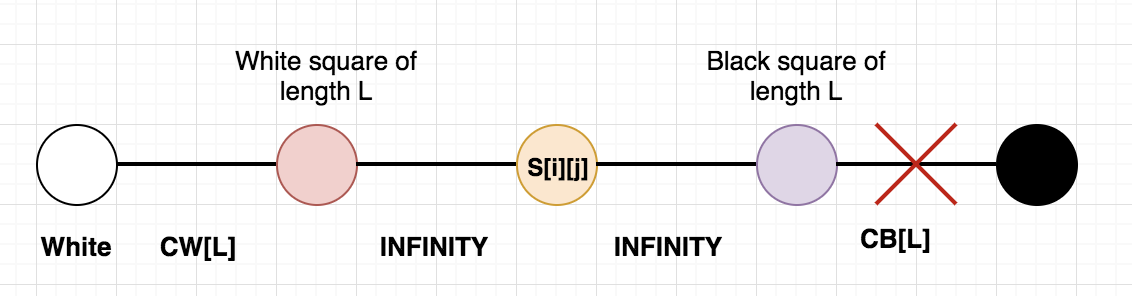
This case is similar to above case, just that instead one of the ? in the optimistic black square of length L chose to convert to 0 instead of 1.
Thus the minimum cut in the above graph will contain edges which tell that the optimistic square which we considered for being white or black will not be actually white or black in the optimal selection because one of ? chose to convert to opposite colour. We must thus remove this minimum optimistic answer we added to “initial ans” to obtain the solution to the problem.
Let us now finally analyse the complexity of the above solution. For the worst case, the grid will only consist of ? as there are no edges coming out of 0 or 1 in the grid. Let K = min(N, M). So there will be N * M + (N - 1) * (M - 1) + \cdots + (N - K) * (M - K) = O(K^3) intermediate white and black nodes i.e. the ones connecting grid cells and also to the corresponding source or sink. For details of the proof, refer to this. The number of edges in the graph will be O(K^4) as there can be maximum O(L^2) edges from an intermediate node representing the square of length L. Using Dinic Algorithm which has the worst complexity of O(V^2 * E), the overall complexity of the solution will be O(K^{10}) ~ O({(N * M)}^3). The hidden constant factor is very low and Dinic’s algorithm suffices to solve the problem.
Extra Observation
Note that above solution using minimum cut also enables us to print one grid with required cost as well. The construction of such grid is simple. Just consider the edges from white (source) and black (sink) node to the intermediate nodes which are not part of the minimum cut. This means all the cells in the grid connected to it actually retained their preference to colour which was optimistically assigned before to them.
Once, you are clear with the above idea, you can see the editorialist implementation below for help. It also contains the part for printing a possible grid with the conversion of ? to 0 or 1.
Author’s Editorial for the problem
Click to view
Consider using the minimum cut algorithm. If n < m, swap them.
Let SB denote the prefix sum of CB, and SW is defined similarly.
We define the map S from integer to integer, where:
-
When i>0 S[i]=SB[i];
-
When i<0 S[i]=SW[-i].
For every grid (i,j), we try to determine the maximum length |l| such that (i,j)-(i+|l|,j+|l|) is a square with solid color. If it is black, l>0; otherwise, l<0.
Thus the answer is sigma{S[l[i][j]]}.
For every (i,j) we create nodes (i,j,l) for -n<=l<=n, and add edges for:
-
For l<0, (i,j,l) → (i,j,l+1) cost = inf - S[l];
-
For l>0, (i,j,l-1) → (i,j,l) cost = inf - S[l];
-
S->(i,j,-n) cost = inf * 2
-
(i,j,n)->T cost = inf * 2
Cutting an edge refers to choosing the corresponding l for (i,j).
Here for certain (i,j), we call the edges described above a “chain”.
The reason for adding an inf to every edge is to avoid the cut having multiple edges on the same chain. However, each (i,j) cannot choose its value “l” arbitrary but must follow some constraints.
We first define dist((i,j),(k,l)) = max{i-k,j-l}.
So the constraints are:
-
When (i,j) is black (i.e. l[i][j] > 0), for k<=i and l<=j: l[k][l] > -dist((i,j),(k,l))
-
When (i,j) is white (i.e. l[i][j] < 0), for k<=i and l<=j: l[k][l] < dist((i,j),(k,l))
-
For every individual (i,j), l[i][j] should take the number with maximum absolute value, while not violating rule 1 and 2.
In the following part we use => sign to denote “lead to” relationship, i.e. A=>B is equivalent to “when A is true, B is true”. So we rewrite rule 1 and 2:
-
l[i][j] > 0 => l[k][l] >= -dist((i,j),(k,l))
-
l[i][j] < 0 => l[k][l] <= dist((i,j),(k,l))
For rule 1, we just link edge : (i,j,0) → (k,l,-dist((i,j),(k,l))) cost = inf * 2
Easy to see that if the rule is violated, there would be an S-T path.
For rule 2, we just link edge (k,l,dist((i,j),(k,l))) → (i,j,0) cost = inf * 2
Easy to see that if the rule is violated, there would be an S-T path.
For rule 3: Every CB[i] and CW[i] is positive, so SB and SW are strictly increasing, thus every certain (i,j) will greedily take the value with maximum absolute value even if we don’t interfere.
Thus, the minimum cut is the answer.
Dinic or ISAP algorithm is recommended and will find the answer very fast.
Feel free to share your approach, if it was somewhat different.
Time Complexity
O({(N * M)}^3)
Space Complexity
O({(N * M)}^3)
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Editorialist’s solution can be found here.