PROBLEM LINK:
Setter- Stepan Filippov
Tester- Teja Vardhan Reddy
Editorialist- Abhishek Pandey
DIFFICULTY:
MEDIUM
PRE-REQUISITES:
Implementation, 2-D prefix sums (check setter’s code for its implementation), Geometry (for visualize rectangle intersection part)
PROBLEM:
Given 2 2-D arrays, of dimensions h_1*w_1 and h_2*w_2, scale them both upto dimensions of lcm(h_1,h_2)*lcm(w_1,w_2) and find number of equal elements in them.
QUICK-EXPLANATION:
Key to AC- The rectangles in this question can intersect in at most 9 ways. Also, there is symmetry. We dont need to consider all rectangles of other photo intersecting a rectangle in fist photo.
Note that by virtue of regularity, there are 9 ways by which rectangles can intersect. The brute force of task 2 counts all the rectangles of other within the rectangle of current photo. We can optimise it further by only considering the 9 types of “representative rectangles”, find their area, and multiply it with number of such rectangles. Rest of all is implementing this idea.
EXPLANATION:
This editorial will have essentially three parts, each dedicated for a subtask. The setter’s code is well commented, and a description of idea along with code snippets will be given in editorial to make sure that you grasp the idea as well as how to convert that idea into code.
First Subtask-
I recall someone once said you people dont like stories and want only the formal stuff ![]() . Ok then, lets skip all the stories and formally state the answer of the first subtask, because everyone likes formal things
. Ok then, lets skip all the stories and formally state the answer of the first subtask, because everyone likes formal things ![]()
Ans=\sum_{i=0}^{h1-1} \sum_{j=0}^{w1-1} \sum_{k=0}^{h2-1} \sum_{l=0}^{w2-1} Intersection(\alpha i,\beta j,\alpha i+\alpha -1, \beta j +\beta -1,\gamma k, \delta l, \gamma k+\gamma -1,\delta l+\delta -1)[p1[i][j]==p2[k][l]]
where-
\alpha=lcm(h1,h2)/h1
\beta=lcm(w1,w2)/w1
\gamma =lcm(h1,h2)/h2
\delta=lcm(w1,w2)/w2
Intersection is a function which takes corner of 2 rectangles and returns their intersection area.
Just find above and we are done with subtask 1!! ![]()
Click to view
Either make new 2-D matrices which are of dimensions lcm(h1,h2) *lcm(w1,w2) (with pixels filled correspondingly as required by question) and compare every pixel, or for every pixel in P1, check all the possible pixel values in P2 and compare them. The above formula does the same thing and is a simple formal representation of it.
Subtask 2-
This can be crossed by optimising the above approach. Check only the rectangles which actually contribute to answer instead of checking all possible pixels in enlarged version of P2. It differs from above brute force in 2 aspects-
- It deals with entire contribution of rectangle at once instead of individual pixels
- Only count rectangles which actually contribute! For a fixed (i,j), if the rectangle contributes, we have constraints on k and l as \lfloor \frac {\alpha i} {\gamma} \rfloor \le k \le \lfloor \frac{\alpha i +\alpha -1}{\gamma} \rfloor and \lfloor \frac {\beta j} {\delta} \rfloor \le l \le \lfloor \frac{\beta i +\beta -1}{\delta} \rfloor. This reduces complexity to O((h1+h2) \times (w1+w2)). For more info, you can refer to attached file in bonus corner. Interested ones can refer to tab below for more details
Click to view
The secret knowledge is hidden somewhere here. Can you find it?
Click to view

Subtask 3-
Now, how can we optimize more?
We are quite clear that if number of rectangles are not much, then our solution of sub-task 2 will work in time. But what if rectangles are too many?
Lets try to get an intuition first. What if number of rectangles are possible? One of the scenarios when its possible is that, rectangles of P1 are huge and rectangles of P2 are very small. Now, try to imagine their intersection and see what subtask 2 algorithm does. For every small rectangle inside the huge rectangle of P1 (in scaled version), it will check if it lies inside, and if yes then add its contribution. Do we need to check all the small rectangles, if we know the length of small and large rectangles? Obviously no! And this is where we will optimize now.
If we know that K rectangles lie fully and a rectangle lying fully has a contribution of, say A to answer, then we can quickly find contribution of all K rectangles by simple multiplication. Read my next sentence very carefully. We can, “abstract” or generalize the above line as, “The contribution of rectangles of type i is j and there are k such rectangles.” (I just replaced the fixed values with variables as placeholders for generalization). This approach can count contribution of all rectangles of a type i at once!
Now, ask how many such “types” can exist? Can it be 2 ? Rectangle completely inside and rectangle partially inside? But “partially inside” sounds a bit vague. How will we actually prove that all those “partially” lying inside rectangles will have equal contribution? Hint: We can’t because its false! This means, we need to further sub-divide this “partially intersecting” type more and more, until we can get definite values of j and k for all types trivially.
Now, multiple such definitions can exist, but the one identified by setter is beautiful. He identified, 9 such possibilities-
- 4 types for rectangles intersecting at the 4 corners.
- 4 types for rectangles intersecting at the 4 sides.
- 1 type for all rectangles lying completely inside.
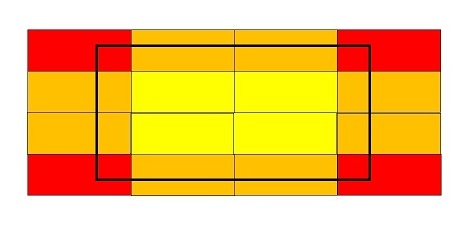
Now, with the 9 identified types, he proceeded to find contribution of each type, and then number of rectangles belonging to each type (looking at his code, we can see that there can be only 1 rectangle intersecting at corner).
Lets see how to elegantly solve this. As usual for clear implementation, we should fist identify the “tools” or functions which we might need to finish the job. Reading the above idea, we get the following requirements-
- A function to tell if rectangles intersect or not. Or even better, given the area of intersection of the rectangles. This is getIntersection() function in setter’s solution, which takes the upper left and bottom right co-ordinates of the two rectangles and gives the area of intersection.
- A function to get a count of how many rectangles of each type are there. Setter used 2-D prefix sum to find this. Basically, Prefix[i][j] would give the number of pixels which are 1 in ORIGINAL (not the scaled!!) photo of P2, and by this we can determine number of pixels which are 0 as well (as sum of ‘0’ and ‘1’ pixels = Area of rectangle defined by indexes (i,j) and (0,0)). A brief explanation of how to calculate this is in my corner, or you can look at setter’s code as well.
Now, the algorithm followed henceforth is quite simple. First, grab the data needed to check which of the 9 cases the rectangle lies in. For each pixel in P1, find the co-ordinates of upper left and bottom-right co-ordinates of rectangle in scaled version. Now, use them to find upper-left and bottom right co-ordinates of rectangle in original (i.e. NOT scaled) array of P2. This data is sufficient for us to make cases now.
An implementation code for above is below if you want to sync it with explanation-
Click to view
for (int i = 0; i < n1; i++)
for (int j = 0; j < m1; j++)//ll= long long , 64 bit data type to prevent overflow
{
ll x1 = i * h1, y1 = j * w1;//Find starting coords
ll x2 = x1 + h1 - 1, y2 = y1 + w1 - 1;//Find diagonally opposite coords
int i1 = x1 / h2, i2 = x2 / h2;//Find corresponding coords in P2
int j1 = y1 / w2, j2 = y2 / w2;
Now, start with your case making.
If the rectangle intersection is of corner-intersection, then we know that count of such rectangles can only be 1, and we can find their contribution by getIntersection() function. A pseudocode to deal with one of the cases (one of the four corners) is given below, try to complete the rest for other 3 directions. (All these snippets are taken from setter’s code, so feel free to refer to it for final answer.)
Click to view
if (a[i][j] == b[i1][j1]) // UL
ans +=get_intersection(x1,y1,x2,y2, i1 * h2, j1 * w2, i1 * h2 + h2 - 1, j1 * w2 + w2-1);
Now, for each of the 4 sides with which rectangles can intersect, we need to find number of such intersections/rectangles AND their contribution. Recall the 2-D prefix sum done earlier. It will be used to ultimately find number of rectangles. For now, since idea is more on syncing explanation and implementation of the idea, lets use get_cnt() function which “does something” with 2-D prefix sum and gives count of rectangles. (You are encouraged to explore what that “does something” is, before checking it out in setter’s code. Its simple < 5 line code. Read my note on 2-D prefix sum’s use for a hint).
Try to come up with code for rectangles intersecting at upper side. Then compare it with abstracted-implementation below, and come up with implementation for other 3 directions.
Click to view
if (j1 + 1 <= j2 - 1) // U
{
int cnt = get_cnt(i1, j1 + 1, i1, j2 - 1);
if (a[i][j] == '0')
cnt = (j2 - j1 - 1) - cnt;
ans += cnt * get_intersection(x1, y1, x2, y2, i1 * h2, (j1 + 1) * w2, i1 * h2 + h2 - 1, (j1 + 1) * w2 + w2 - 1);
}
(Beware: Make sure not to over count rectangles in case the dimensions are 1*N or N*1 types. You must not count same rectangles in “intersecting with upper side” and “intersecting with lower side” etc. Count them only once!)
Now what is left is the code for rectangles lying completely in the centre. Feeling upto the challenge? Can you use the tools defined so far to come up with that WITHOUT overcounting?
Click to view
// Count centre
if (i1 + 1 <= i2 - 1 && j1 + 1 <= j2 - 1)
{
int cnt = get_cnt(i1 + 1, j1 + 1, i2 - 1, j2 - 1);
if (a[i][j] == '0')
cnt = (i2 - i1 - 1) * (j2 - j1 - 1) - cnt;
ans += cnt * get_intersection(x1, y1, x2, y2, (i1 + 1) * h2, (j1 + 1) * w2, (i1 + 1) * h2 + h2 - 1, (j1 + 1) * w2 + w2 - 1);
}
SOLUTION
Click to view
#include <stdio.h>
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1000000;
ll gcd(ll x, ll y)
{
while (x)
{
y %= x;
swap(x, y);
}
return y;
}
ll lcm(ll x, ll y)
{
return x * y / gcd(x, y);
}
// The area of intersection of rectangles [(x1, y1), (x2, y2)] and [(x3, y3), (x4, y4)]
ll get_intersection(ll x1, ll y1, ll x2, ll y2, ll x3, ll y3, ll x4, ll y4)
{
ll dx = max(0LL, min(x2, x4) - max(x1, x3) + 1);
ll dy = max(0LL, min(y2, y4) - max(y1, y3) + 1);
return dx * dy;
}
string a[N], b[N];
vector<int> sum[N + 1];
/*
sum[i + 1][j + 1] =
b[0][0] + ... + b[0][j]
+ +
. .
+ +
b[i][0] + ... + b[i][j]
*/
void build_sum(int n, int m)
{
for (int i = 0; i < n + 1; i++)
{
sum[i].resize(m + 1);
fill(sum[i].begin(), sum[i].begin() + m + 1, 0);
}
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
sum[i + 1][j + 1] = (b[i][j] - '0');
for (int i = 0; i < n + 1; i++)
for (int j = 1; j < m + 1; j++)
sum[i][j] += sum[i][j - 1];
for (int i = 1; i < n + 1; i++)
for (int j = 0; j < m + 1; j++)
sum[i][j] += sum[i - 1][j];
}
// The sum of values in a rectangle [(x1, y1), (x2, y2)]
int get_cnt(int x1, int y1, int x2, int y2)
{
return sum[x2 + 1][y2 + 1] - sum[x1][y2 + 1] - sum[x2 + 1][y1] + sum[x1][y1];
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cout.precision(20);
cout << fixed;
int T;
cin >> T;
while (T--)
{
string tmp;
int n1, m1;
cin >> n1 >> m1;
cin >> tmp;
for (int i = 0; i < n1; i++)
a[i] = tmp.substr(i * m1, m1);
int n2, m2;
cin >> n2 >> m2;
cin >> tmp;
for (int i = 0; i < n2; i++)
b[i] = tmp.substr(i * m2, m2);
build_sum(n2, m2);
ll H = lcm(n1, n2), W = lcm(m1, m2);
ll h1 = H / n1, w1 = W / m1;
ll h2 = H / n2, w2 = W / m2;
ll ans = 0;
for (int i = 0; i < n1; i++)
for (int j = 0; j < m1; j++)
{
ll x1 = i * h1, y1 = j * w1;
ll x2 = x1 + h1 - 1, y2 = y1 + w1 - 1;
int i1 = x1 / h2, i2 = x2 / h2;
int j1 = y1 / w2, j2 = y2 / w2;
// We consider the pixel (i,j) from the first photo
// It corresponds to a rectangle [(x1, y1), (x2, y2)] in the upscaled photo.
// Count corners
if (a[i][j] == b[i1][j1]) // UL
ans += get_intersection(x1, y1, x2, y2, i1 * h2, j1 * w2, i1 * h2 + h2 - 1, j1 * w2 + w2 - 1);
if (i2 != i1 && a[i][j] == b[i2][j1]) // DL
ans += get_intersection(x1, y1, x2, y2, i2 * h2, j1 * w2, i2 * h2 + h2 - 1, j1 * w2 + w2 - 1);
if (j2 != j1 && a[i][j] == b[i1][j2]) // UR
ans += get_intersection(x1, y1, x2, y2, i1 * h2, j2 * w2, i1 * h2 + h2 - 1, j2 * w2 + w2 - 1);
if (i2 != i1 && j2 != j1 && a[i][j] == b[i2][j2]) // DR
ans += get_intersection(x1, y1, x2, y2, i2 * h2, j2 * w2, i2 * h2 + h2 - 1, j2 * w2 + w2 - 1);
// Count sides
if (j1 + 1 <= j2 - 1) // U
{
int cnt = get_cnt(i1, j1 + 1, i1, j2 - 1);
if (a[i][j] == '0')
cnt = (j2 - j1 - 1) - cnt;
ans += cnt * get_intersection(x1, y1, x2, y2, i1 * h2, (j1 + 1) * w2, i1 * h2 + h2 - 1, (j1 + 1) * w2 + w2 - 1);
}
if (i1 + 1 <= i2 - 1) // L
{
int cnt = get_cnt(i1 + 1, j1, i2 - 1, j1);
if (a[i][j] == '0')
cnt = (i2 - i1 - 1) - cnt;
ans += cnt * get_intersection(x1, y1, x2, y2, (i1 + 1) * h2, j1 * w2, (i1 + 1) * h2 + h2 - 1, j1 * w2 + w2 - 1);
}
if (j1 + 1 <= j2 - 1 && i1 != i2) // D
{
int cnt = get_cnt(i2, j1 + 1, i2, j2 - 1);
if (a[i][j] == '0')
cnt = (j2 - j1 - 1) - cnt;
ans += cnt * get_intersection(x1, y1, x2, y2, i2 * h2, (j1 + 1) * w2, i2 * h2 + h2 - 1, (j1 + 1) * w2 + w2 - 1);
}
if (i1 + 1 <= i2 - 1 && j1 != j2) // R
{
int cnt = get_cnt(i1 + 1, j2, i2 - 1, j2);
if (a[i][j] == '0')
cnt = (i2 - i1 - 1) - cnt;
ans += cnt * get_intersection(x1, y1, x2, y2, (i1 + 1) * h2, j2 * w2, (i1 + 1) * h2 + h2 - 1, j2 * w2 + w2 - 1);
}
// Count centre
if (i1 + 1 <= i2 - 1 && j1 + 1 <= j2 - 1)
{
int cnt = get_cnt(i1 + 1, j1 + 1, i2 - 1, j2 - 1);
if (a[i][j] == '0')
cnt = (i2 - i1 - 1) * (j2 - j1 - 1) - cnt;
ans += cnt * get_intersection(x1, y1, x2, y2, (i1 + 1) * h2, (j1 + 1) * w2, (i1 + 1) * h2 + h2 - 1, (j1 + 1) * w2 + w2 - 1);
}
}
cout << ans << "\n";
}
return 0;
}
Click to view
//teja349
#include <bits/stdc++.h>
#include <vector>
#include <set>
#include <map>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <climits>
#include <utility>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <iomanip>
//setbase - cout << setbase (16); cout << 100 << endl; Prints 64
//setfill - cout << setfill ('x') << setw (5); cout << 77 << endl; prints xxx77
//setprecision - cout << setprecision (14) << f << endl; Prints x.xxxx
//cout.precision(x) cout<<fixed<<val; // prints x digits after decimal in val
using namespace std;
#define f(i,a,b) for(i=a;i<b;i++)
#define rep(i,n) f(i,0,n)
#define fd(i,a,b) for(i=a;i>=b;i--)
#define pb push_back
#define mp make_pair
#define vi vector< int >
#define vl vector< ll >
#define ss second
#define ff first
#define ll long long
#define pii pair< int,int >
#define pll pair< ll,ll >
#define sz(a) a.size()
#define inf (1000*1000*1000+5)
#define all(a) a.begin(),a.end()
#define tri pair<int,pii>
#define vii vector<pii>
#define vll vector<pll>
#define viii vector<tri>
#define mod (1000*1000*1000+7)
#define pqueue priority_queue< int >
#define pdqueue priority_queue< int,vi ,greater< int > >
//std::ios::sync_with_stdio(false);
ll possw[2123456],possh[2123456],pre[1234567];
string s1,s2;
int main(){
std::ios::sync_with_stdio(false);
ll t;
cin>>t;
while(t--){
ll h1,w1;
cin>>h1>>w1;
cin>>s1;
ll h2,w2;
cin>>h2>>w2;
cin>>s2;
if(w2<w1){
swap(w1,w2);
swap(s1,s2);
swap(h1,h2);
}
pre[0]=s2[0]-'0';
ll i=0;
// calculating prefix sums assuming it is a 1d figure (we can always prefix sum of any 1d row segment from this)
f(i,1,h2*w2){
pre[i]=pre[i-1]+s2[i]-'0';
}
ll gh,lh,fh1,fh2;
gh=__gcd(h1,h2);
lh=h1*h2/gh;
fh1=lh/h1;
fh2=lh/h2;
ll gw,lw,fw1,fw2;
// gcd
gw=__gcd(w1,w2);
// lcd
lw=w1*w2/gw;
// multiplier1
fw1=lw/w1;
// multiplier 2
fw2=lw/w2;
i=0;
ll j=0;
ll val=0;
ll k=0;
// point of changes for width
while(val<lw){
possw[k] = val;
k++;
i++;
val+=fw1;
}
possw[k]=lw;
k++;
ll sizw=k;
i=0;
j=0;
val=0;
k=0;
// point of changes for ht.
while(val<lh){
if(val==i*fh1){
possh[k] = val;
k++;
i++;
if(val==j*fh2){
j++;
}
}
if(val==fh2*j){
possh[k] = val;
k++;
j++;
}
val=min(j*fh2,i*fh1);
}
possh[k] = lh;
k++;
ll sizh = k;
ll mulh,mulw,haha1,haha2,wow1,wow2,pos1,pos2;
ll poss2,lefo,rigo,rig,lef;
ll gg;
ll ans=0,tot=0;
//iterating over point of changes of ht.
rep(j,sizh-1){
mulh=possh[j+1]-possh[j];
haha1=possh[j]/fh1;
haha2=possh[j]/fh2;
haha1*=w1;
haha2*=w2;
ans=0;
// iterating over point of changes of smaller width and using prefix sums to find answer over these.
rep(i,sizw-1){
gg=0;
wow1=possw[i]/fw1;
pos1=haha1+wow1;
mulw=possw[i+1]-possw[i];
rig=possw[i+1]-1;
lef=possw[i];
lefo=lef/fw2;
rigo=rig/fw2;
if(lefo!=rigo){
poss2=haha2+lefo;
gg=(s2[poss2]-'0')*(lefo*fw2+fw2-lef);
poss2=haha2+rigo;
gg+=(s2[poss2]-'0')*(rig-rigo*fw2+1);
rigo--;
lefo++;
if(lefo<=rigo)
gg+=(pre[haha2+rigo]-pre[haha2+lefo-1])*fw2;
if(s1[pos1]=='0'){
ans+=mulw-gg;
}
else{
ans+=gg;
}
}
else{
poss2=haha2+lefo;
if(s1[pos1]==s2[poss2])
ans+=mulw;
}
}
tot+=ans*mulh;
}
cout<<tot<<'\n';
}
return 0;
}
Editorialist
Time Complexity=O(N*M)
Space Complexity=O(N*M)
CHEF VIJJU’S CORNER 
1. Shoutout for Steppan!
Click to view
This section is here just to appreciate this setter. Do you guys know, that when I asked the setters to comment their codes for readability and submit the same on campus, he was the first one to do so! Also, his notes are very beautifully written. They are crisp, and they capture the essence of solution. Just to let everyone know, he is one of the setters we all should appreciate for his discipline and professionalism ![]()

2. How to find 2-D prefix sum and its use-
Click to view
The algorithm to find 2-D prefix sum is actually, quite simple! In fact, it has only 3 steps-
- Initialize your 2-D array.
- Find prefix sum along the rows, i.e. for each row find prefix sum (like we do for normal arrays).
- Find prefix sum along the columns.
A commented implementation is in below tab-
Click to view
void build_sum(int n, int m)
{
for (int i = 0; i < n + 1; i++)//Initialize all values to 0. Optional.
{
sum[i].resize(m + 1);
fill(sum[i].begin(), sum[i].begin() + m + 1, 0);
}
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
sum[i + 1][j + 1] = (b[i][j] - '0');//Initialize the array
for (int i = 0; i < n + 1; i++)
for (int j = 1; j < m + 1; j++)
sum[i][j] += sum[i][j - 1];//Prefix sum along row
for (int i = 1; i < n + 1; i++)
for (int j = 0; j < m + 1; j++)//Prefix sum along column
sum[i][j] += sum[i - 1][j];
}
Now, with this definition of 2-D prefix sum, we can say that Prefix[i][j]-Prefix[a][b] will give count of value (which we prefixed) in rectangle defined by opposite corners (i,j) and (a,b)
3. Hall of Fame for Noteworthy Solutions-
- By karolis_kusas
- um_nik
- Who can be next???
Can see your code here? Give me a link to check it up and add ![]()
 . Perhaps discuss doesnt want my editorials wikified. Not that I have a problem with that >:-) XD
. Perhaps discuss doesnt want my editorials wikified. Not that I have a problem with that >:-) XD
