PROBLEM LINK:
Setter- Misha Chornyi
Tester- Teja Vardhan Reddy
Editorialist- Abhishek Pandey
DIFFICULTY:
CHALLENGE
PRE-REQUISITES:
General Programming. Knowledge of Probability and Expectations
PROBLEM:
Given a N*M matrix, divide it into K connected components such that |Max-Min| is minimized, where Max is the maximum valued component and Min is minimum valued component.
QUICK-EXPLANATION:
Key to AC- Notice that numbers are uniformly, randomly generated. Trying out various orderings and simulations was expected to give good score.
Note that the values are uniformly, randomly generated. Hence, if we divide the array into \frac{N*M}{K} partitions, then it;d be a good start. Lets see what more we can do. Assign labels to array elements such that elements of same labels are in same connected component. Now, try to convert it into a 1-D array and see if we can do manipulations (eg- push another element into minimum district subarray). Trying out multiple such labellings/orderings/patterns and operating ideally on them was expected to give a good score.
EXPLANATION:
I will be sharing the expected solution of setter in the editorial. As usual, the editorial of challenge problem is never complete without contribution from community. So if you have any approach which is not yet covered, feel free to share it! ![]()
Setter’s solution is quite simple and relies on the fact that numbers are randomly generated, so its very unlikely that theres a huge concentration of high or low values accumulated around a small area.
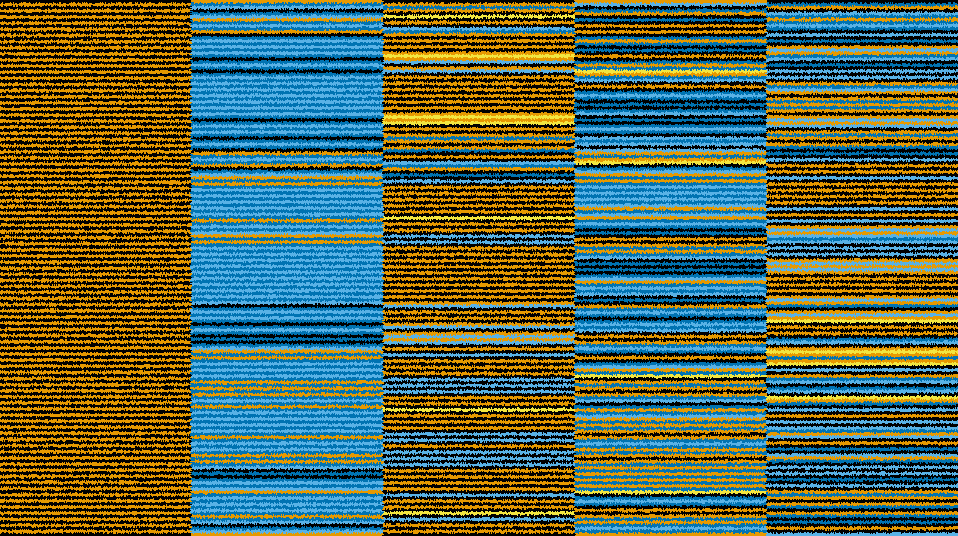
I tried to visualise the process in pic below, before beginning to explain it.

The first step in the above algorithm would be, to try any random order. One property which must hold in that order is that, elements which are adjacent in the equivalent 1-D array must also be adjacent in the initial 2-D array as well. You can try multiple such orders, for example, in the picture above I followed the order/pattern of going from left to right, then 1 step down, then right to left … and so on.
Now, for every order you try, assign the matrix elements “labels” or indices where they’d appear in 1-D array. Once done, convert the 2-D array into 1-D array. Now our problem reduces to “Partition a 1-D array into atmost K partitions such that difference between highest and lowest valued partition is minimum.”. Note that, following just 1 or 2 patterns may not give optimal answer, we simulate the process for multiple patterns/orderings. (Meaning, steps till now are simulated for multiple patterns).
One way of initially partitioning the array could be, find the array sum and partition whenever the size of partition is \approx N*M/K, other would be to partition when the partition sum is close to \sum A_{ij}/K. Another very good improvement is, once we get an initial partition, try “popping an element out of maximum partition” and/or “pushing an element into minimum partition” (since we made sure that elements adjacent in 1-D array are adjacent in 2-D matrix as well, its well possible). Do this as long as it helps.
However, note that our algorithm has an expensive step, determine and assign partition. That step takes O(N*M) time, while manipulating the already partitioned array (pushing/popping as discussed before) takes significantly less time. So, its worthwhile to pay some extra attention in trying to improve manipulation techniques rather than blindly using thousands of orderings/patterns.
Thats it from setter’s side XD. I tried to decode participants solutions but most of the top solutions are complex ![]() . I’d hence like to invite everybody to share their approach and how it ended up for them. Hope you guys enjoyed the problem.
. I’d hence like to invite everybody to share their approach and how it ended up for them. Hope you guys enjoyed the problem.
SOLUTION
Click to view
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef long double dbl;
typedef vector <int> vi;
typedef pair <int, int> pii;
int const N = 1002;
int const MD = 1000000007;
#define FOR(i, a, b) for (int (i) = (a); (i) <= (b); ++(i))
#define RFOR(i, a, b) for (int (i) = (a); (i) >= (b); --(i))
#define REP(i, n) FOR(i, 0, n - 1)
#define pb push_back
#define mp make_pair
#define X first
#define Y second
#define sz(v) int(v.size())
int res[N][N];
int main() {
int N, M, K;
scanf("%d%d%d", &N, &M, &K);
vector <pii> parts;
FOR (i, 1, N) {
FOR (j, 1, M) {
if (i & 1) {
parts.pb(mp(i, j));
} else {
parts.pb(mp(i, M - j + 1));
}
}
}
int X = (N * M) / K;
int ptr = 0;
FOR (it, 1, (N * M) % K) {
FOR (i, 1, X + 1) {
res[parts[ptr].X][parts[ptr].Y] = it;
++ptr;
}
}
FOR (it, (N * M) % K + 1, K) {
FOR (i, 1, X) {
assert (ptr < sz(parts));
res[parts[ptr].X][parts[ptr].Y] = it;
++ptr;
}
}
assert (ptr == sz(parts));
FOR (i, 1, N) {
FOR (j, 1, M) {
printf("%d%c", res[i][j], j == M ? '\n' : ' ');
}
}
return 0;
}
Tester
Editorialist
Time Complexity=O(N*M)
Space Complexity=O(N*M)
CHEF VIJJU’S CORNER 
1. Setter’s Notes-
Click to view
I expected something like partition N*M in components with approximately equal size [N*M]/K
Several times. As distribution is uniform it’s OK.So, you can move some element from one district to another. When you find some partition Then let’s try to increase the population in the minimal populated district Or decrease the population in the maximal populated district.
2. Hall of fame for noteworthy Solutions
-
mcfx1 - This bad boy made us change the scoring function during contest :(. Shoutout at his crisp 852 line code!

- whzzt - Best solution in terms of score and memory. His code is \approx 180 lines.
-
gorre_morre - GORRE MORRE STRIKES BACK!!
 XDD. This time with a crisp 629 line code in python.
XDD. This time with a crisp 629 line code in python. - algmyr - The guy in class who scores 99\% (Hint: Check his score).
3. A note on when questions have this random generation-
Click to view
There are multiple times when you’ll come across a question quoting “test data is randomly generated.” Usually, for such problems, one thing to keep in mind is, that usually the worst case of an algorithm is HIGHLY unprobable. Like, in DARTSEGM, a problem which I shared below, the expected size of convex hull when points are randomly generated is O(logN). This does not mean that for all arrangements it holds, we can make an arrangement when the size is O(N), i.e. all points are part of hull, but what it means is that, since expected size is O(LogN), then a huge deviation from it is NOT expected if test data is generated randomly. In other words, the worst case may (or usually will) not occur among the test data. With this in mind, you can try going forward to such questions from now on. Remember, “test data randomly generated” is the keyword, dont try this if this isnt guaranteed! XD
4. Related Problems-
- DARTSEGM - Randomly Generated. Enough said. XD









 )
)