PROBLEM LINK:
Setter: Hasan Jaddouh
Tester: Misha Chorniy
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Partial sums on a grid, implementation skills, and Manhattan distance. Visualization skills would be an advantage.
PROBLEM:
Given a N*M grid consisting of 0 and 1 only, Find the number of pairs of 1s in this grid having Manhattan distance x for every 1 \leq x \leq N+M-2.
SUPER QUICK EXPLANATION
- Notice that for a position, all positions at Manhattan distance x form a Diamond shape.
- Maintain Partial sums on diagonals, Iterate overall position for every length, counting the number of 1s lying at distance Length (on this diamond) in constant time using partial sums.
- Handle corners of diamond separately, and Indices carefully.
EXPLANATION
For this problem, Brute force solution would be to iterate over every pair of position and check if both positions contain 1. If yes, Increase Number of pairs with Manhattan distance x by 1, if x is Manhattan distance between both positions.
It can be referred in following pseudo-code.
for a in range (0, n): for b in range (0, m): for c in range(0,n): for d in range(0,m): //We are iterating over every pair of position //Current pair of position is ((a,b), (c,d)) if grid[a][b] == 1 and grid[c][d]==1 ans[abs(a-c)+abs(b-d)]++
Clearly, the above solution is of complexity O((N*M)^2) and thus, will time out for the last sub-task.
So, we need to optimize it. (Just see how many complications we like for getting AC :D)
As usual, Intensive Implementation problem ahead, you have been warned.
Suppose we approach the problem lengthwise.
Consider position (x,y) in grid. List all positions in the grid which are at L Manhattan distance from this position.
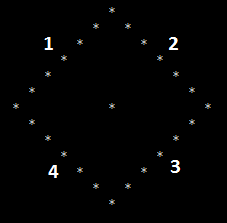
This shape will automatically appear. So, If we count the number of 1s lying on this diamond in constant time, our problem is immediately solved.
But, The Important thing is, How to count?
The usual trick we used to do for find sum of sub-array when the array is static, that is Partial sums (Commonly used partial sums include Prefix arrays).
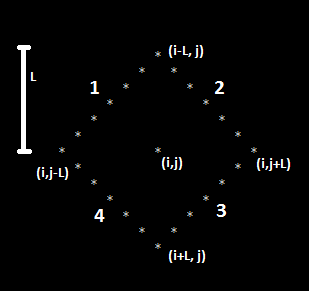
Now, we will split the diamond into 4 lines (We will handle corner points of diamond later). We will try to count the number of 1s lying on each line. For this purpose, we need partial sums on each diagonal of the grid. We have two type of diagonals, One from top left to bottom right (Called LTR (Left-to-Right) diagonal) and Top-Right to Bottom Left (Called RtL diagonal). We can see that line 1 and 3 in the image is of type RTL while line 2 and 4 in the image are of type LtR.
After we get the number of 1s on each line, we can see that if there is 1 on any corner point, it will be counted twice, so, we check if corner point as 1, and if yes, exclude it once to get the accurate count.
Now, the Final answer will contain double the number of pairs with Manhattan distance x for every 1 \leq x \leq N+M-2 Since each pair is counted twice, So, just divide final answers by 2.
Since this is an implementation problem, I am sharing a few implementation points too.
Building partial sum arrays on diagonal.
Click to view
Consider we are making for Diagonal of type LtR first. Recurrence for building LtR partial sum grid is LR[i][j] = g[i][j] + LR[i-1][j-1]. This way, LR[i][j] represent number of 1s on diagonal of type LtR ending at (i,j).
For partial sum grid of type RtL, recurrence is RL[i][j] = g[i][j]+RL[i-1][j+1]
For Handling lines, a picture for understanding.
Click to view
I know that problem still require careful implementation to avoid Index out of bounds error, but that’s what an implementation problem is.
Implementaton
First of all, the preprocessing matrix can be reflected as follows.
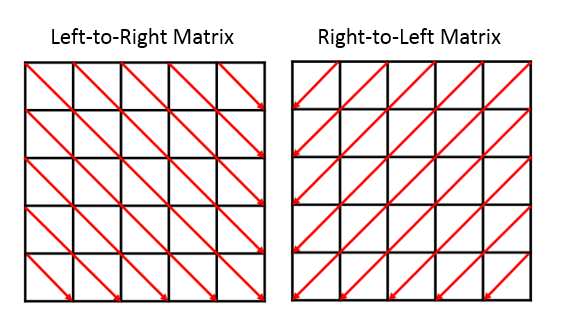
Every position ltr[x][y] and rtl[x][y] contains the sum of elements, which are passed by the arrow to reach position (i,j). This array can be simply calculated using recurrences I mentioned above.
Very very Important part about these matrices, is to learn how to move z positions up and down. (0-based indexing in the grid).
For LTR matrix, each red diagonal satisfies y = x+C for some constant C ranging from -N+1 to M+1. If any point has y-x outside this range, The diagonal crossing that point can never touch grid at all and can be ignored. Suppose we are at (x, y) and want to move two steps downward, to include z cells on same diagonal in next z rows. We know, the new X coordinate will be x+z. New y coordinate is (x+z)+C.
For RTL matrix, each red diagonal satisfies y = -x+C for some constant C ranging from 0 to N+M-2. If any point has x+y outside this range, The diagonal crossing that point can never touch grid at all and can be ignored. Suppose we are at (x, y) and want to move z step downward, to include z cells on same diagonal in next z rows. We know, new X-coordinate will be x+z. New y coordinate is (x+z)-C.
Be sure to understand this part, only then next will make sense.
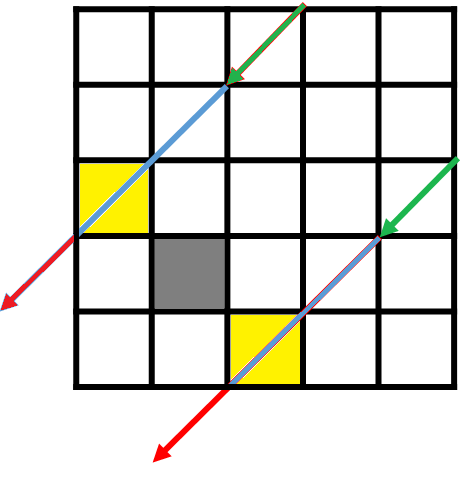
Let’s start actual counting of pairs. Suppose we want to calculate the number of 1s lying on Diamond shape formed by all positions at Manhattan Distance L from (x,y).
We split the work into four diagonals of diamond, and use prefix sums. Out of the total diagonal shown image, we count only 1s lying on the red and blue part. But the red part is lying outside the grid, so cannot contain 1 at all. So, for every diagonal, we need the number of 1s lying on the blue part of diagonal.
For example, consider the following image, where the Current position is (4,4) and current length we are solving for is 2. We want to include the positions which have the arrow of color blue passing through them. This is for Two LTR diagonals. The red line is corresponding the imaginary position outside the grid, which is to the right (and bottom) to the current position, at distance L.

The yellow box is the first position in the matrix, which is lying on the path from our imaginary square. Since there cannot be 1 outside grid, the Yellow box will also contain the same number of 1s as the imaginary target box. Consider diagonal bottom to left only. We can find the coordinate of the bottom cell at L distance from (x,y) as (x+L, y) and we know, the yellow cell, lies inside the grid, so, may have min(N-1, x+L) row.
Now, you know one coordinate of the final position, as well as both coordinates of initial position, so, apply what we learned above, moving steps in the matrix.
A similar explanation holds for RTL matrix as well, except that directions are flipped.
(Just Flipped the previous image. xD)
Another thing, the above examples had only target point outside the grid. If the cell having a green arrow is outside grid, we can just ignore it because It can never have non-zero numbers of 1s.
I just cannot explain everything, so, in case you still find any difficulty, please refer solutions below, or ask in comments.
Time Complexity
For every length from 1 to N+M-2, Time to iterate over grid is O(N*M) each, So, overall Time complexity is O((N+M)*N*M). Other preprocessing is of order O(N*M).
So, Final time complexity is O((N+M)*N*M).
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Editorialist’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()

