PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Alei Reyes
Tester: Aleksa Plavsic
Editorialist: Taranpreet Singh
DIFFICULTY:
Hard
PREREQUISITES:
Centroid Decomposition, Disjoint-Sets, Geometry and a knack of implementation.
PROBLEM:
Given an N sided polygon on a 2-Dimensional plane with points numbered from 1 to N given in clockwise order, we are to process Q queries.
- Join points numbered u and v.
- Print area of the region where point (x, y) is lying. In case point lies on some border or outside the polygon, print 0.
QUICK EXPLANATION
- Divide polygon on triangles by all diagonals we have, and maintain a disjoint set for each triangles storing area of regions in the current union of the set of triangles.
- Apply centroid decomposition on tree formed by adding edge between two vertices corresponding to triangles, which share a diagonal.
- Answer queries in reverse order, initially all regions split into triangles, getting merged into larger components and answering queries.
- Handle points carefully which lie on borders whether yet removed or not.
EXPLANATION
This problem is a complicated implementation (been saying that a lot lately, but what can I do? :P)
First of all, Geometry Time
Check if a point P lies on line segment joining A and B.
Click to view
Length of segment AP + length of segment PB = length of segment AB is the sole condition which guarantees that Point P lies on line segment AB.
More details here.
Check if a point P lies inside triangle ABC if vertices are given in clockwise order.
Click to view
Two methods, One is to check for every edge of the triangle in clockwise order, if the point P lies on or to the left of any edge, Point is not strictly inside the triangle.
Second method is based on relation that a(PAB)+a(PAC)+a(PBC) = a(ABC) where a(XYZ) denote area of triangle XYZ.
More details can be found here.
Area of triangle ABC, given coordinates of A(Ax, Ay), B(Bx, By) and C(Cx, Cy).
Click to view
One common formula is abs(Ax*(By-Cy)+Bx*(Cy-ay)+Cx*(Ay-By))/2.
Another formula (as used by setter) is abs((Bx-Ax)*(Cy-Ay)-(Cx-Ax)*(By-Ay))/2
Side information, calculation of the area of a N sided polygon can be done using Shoelace Formula, which can be found here
The first formula is just the shoelace formula for N = 3.
About Triangles.
For any polygon, we can represent it as the union of a number of non-overlapping triangles by joining non-adjacent vertices of the polygon.
See image for example
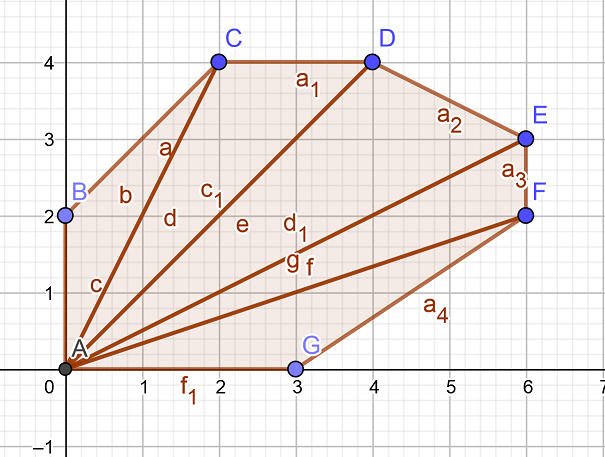
The polygon with N vertices is decomposed into N-2 triangles. Also, all triangles do not overlap, thus the area of the polygon is just sum of areas of all these triangles.
So, Beginning with our approach, let us reverse all queries. The problem looks like following.
We now have a polygon having N vertices with some fences added and we have to process two type of queries.
- Remove fence joining vertices u and v.
- Print the area of the region containing point (x,y).
Though the problem looks still similar, we will see how it is beneficial to merge triangles rather than to split, by using Disjoint set Union, Each set initially consisting of one triangle initially, and another array storing areas of the triangles. When we remove a diagonal, Exactly two sets will merge, the regions, which were earlier divided by that diagonal. Areas also get merged.
The real benefit of reversing queries is because it is far easier to get the area of the region, given area of sub-parts. Rather than finding the area of subregions formed due to new diagonal.
Now, we have all small tools ready for solving this problem. By using all these tools, it is possible to solve this problem in O(N*Q) by answering area queries in O(N) by checking all triangles. If point lie inside any triangle, we can print area of the region which contains this triangle. Otherwise, if the query point lies on any fence, we need to check if this fence was removed. If yes, print area of the region. Otherwise, print 0.
Now, O(N*Q) is too slow to solve our problem, so we need an insight about Polygon Triangulation
If we have a graph of N-2 vertices each representing a triangle, and edge (A, B) for all A \neq B exist if triangle A and triangle B share an edge (not just corner), we get a tree.
Also, consider the following image (Image credits to problem setter).
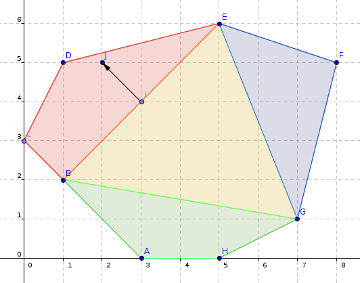
The yellow region is connected to all regions while no other regions are connected with each other. Also, If we know, that query point say J in the image, is lying to the left of segment DE, We can just ignore Blue and Green Regions, and move toward Red region.
Now, we have a tree of regions.
This gives us a different implementation to answer queries in O(N) worst case. (will be helpful to reach our final solution.)
For every query, just choose any triangle, check if query point lies inside that triangle. If yes, print area of the region containing that triangle. Otherwise, there will be one edge of this triangle, from which query point lies to the left side of the edge. Call this Special Diagonal Move toward triangle which shares special diagonal with current triangle. Continue this process until you reach the triangle which contains this triangle, or it is determined that point is outside the polygon.
It is guaranteed that you’ll visit all the triangles in the worst case. Also, make sure to check if a point lies on the border of any triangle. If that border is removed, print area of the region containing that border. Otherwise, print 0.
This way too, we get O(Q*N) time complexity, but this forms the base for optimizing this solution faster than a blink of an eye, just by Divide and Conquer Technique.
Now, in this solution, once we move from one triangle to other, we never move back, thus reducing the size of search space by at least half the size of current search space, if we apply Divide and Conquer on trees, commonly known as Centroid Decomposition on tree, can read here.
We still do the same thing, Choose a starting triangle, check if the point lies inside or on the border of this triangle. If no, we move toward component toward which has the next triangle.
The thing about divide and conquer is, that we have almost the same idea, but just by choosing vertices carefully, we divide the search space into half at every step, resulting in O(logN) steps.
This complexity, combined with O(logN) for usage of maps and other data structures, gives overall O(Q*log^2 N) time complexity which is sufficient to fit the time limit.
As for implementation, I have added line-by-line comments in setter’s solution which you may refer for implementation.
Time Complexity
Time complexity is O(Q*log^2 N).
AUTHOR’S AND TESTER’S SOLUTIONS:
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()