PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Hasan Jaddouh
Tester: Teja Vardhan Reddy
Editorialist: Taranpreet Singh
DIFFICULTY:
Medium-hard
PREREQUISITES:
Simulation, LCA in O(logN) and case based implementation.
PROBLEM:
Given a tree with N vertices and paths of two people of lengths K and L respectively, each person moving at one vertex per unit time. Count the number of times each person meet at any vertex. If paths of any person end, consider him disappeared after next second. (like magic :D)
SUPER QUICK EXPLANATION
- If the distance of starting vertices of both persons is odd, they can never meet, hence answer is zero.
- We break paths of each person into two parts, one going up, and other going down. Now, cases where paths are moving in same or opposite directions separately.
- We now consider the next vertex of both persons, and if one person’s vertex is farther than the other’s, we find a vertex which lies on the path of the person with bogger path, and has distance same as the length of smaller length. This way, we split the path, to make current move length same for both persons.
- If both persons are moving in the opposite direction, they can meet only at one vertex, if they meet.
- If both persons are moving in the same direction and are moving up, they can meet at their LCA till their target vertex for the current move if and only if their target vertices are same.
- If both persons are moving in same direction and are moving down, they should be at same initial vertex to meet, and will share path till LCA of target of both persons.
EXPLANATION
First of all, I am going to prove, that if intital distance between the persons is odd, they can never meet. This happens, because at every move, the distance between them either remain same, or change by two. This way, if initial distance is odd, it can never be zero, that is, they can never meet. So after reading input, print zero directly. (I like such cases :P)
So, we can assume initially, both persons are at even distance.
Consider following image.
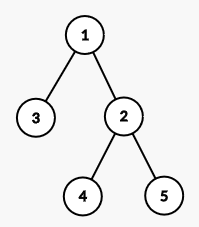
Consider path of one person from 3 to 5. Person moves from 3-1-2-5.
We can see, that LCA(3,5) is 1. If we split path 3 to 5 into two parts 3 to 1 and 1 to 5, the person’s path will not change. The path will still be 3-1-2-5. But the benefit of splitting this path is, that path 3-1 is a path moving upwards, while path 1-2-5 is a path moving downward. This will benefit us later.
In case LCA of u and v is either u or v (this happens when u is in subtree of v, or v is in subtree of u.), we do not add LCA(u, v), becuase the path is already moving in a single direction. Like, if the path is already 1 to 5, we do not make it 1-1-2-5, but let it remain as 1-2-5.
Now, Let us consider a slow solution.
We know, that we can find the direction of movement between any two ajdacent positions by comparing depths. If next vertex has depth less than current vertex, we are moving upward, while if the depth of next vertex is more than depth of current vertex is more than that of current vertex, we are moving downward.
For first subtask, it allows us O(N) time per move, so, we can just maintain two pointers, one for each person indicicating its position at current time. We can find out next vertex where current person moves by using LCA.
Important thing to note here is, that we can find ith vertex from u to root, but we cannot fing ith vertex on path from root to x efficiently. So, suppose d is depth of x and depth of root is 0, then ith vertex from root on path of x is same as (d-i)th vertex from x to root (excluding x). This concept is important. If i need to move to ith parent of x, i’ll say lift x to its ith parent ofr rest of editorial.
This way, we can move both persons and check if their position is same.
The worst case time complexity of this solution is O((K+L)*N*logN). Consider linear tree of type 1-2-3-\dots-N, and at every step, we have to move from 1 to N or vice versa. We will have to move N length path for each move, and there are total (K+L) moves. We also use LCA queries which take O(logN) time.
Clearly, we need a faster approach.
See, we will move each of the (K+L) step in constant time.
We have the paths split as i explained above. Now consider the following tree.
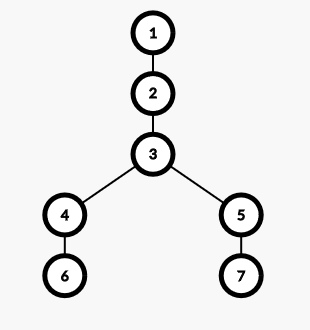
Suppose first person has to move from 6 to 1 while second person has to move from 1 to 5 in current step. We can see, that step length of first person is 5 while step length of second person is 4. So, we can split path of first person, into two parts, that is, first part having length 4, and remaining part the balance. Hence, we split path 6-4-3-2-1 into 6-4-3-2 and 2-1. So, we can for now, consider steps of first person as from 6 to 2, and from 1 to 5 for second person. We will consider the remaining part 2-1 with next step of second person.
So, now we have steps of both persons of equal length. Say from 6 to 2 for first person and from 1 to 5 for second person. We can see that in this case, one person is moving down while other person is moving up.
So, we can assume, that both person has to move same length in current step. We can always split paths to ensure this.
Now, There are two cases to handle.
Both persons are moving in opposite direction at current step.
In this case, if the person moving down is already at lower depth than other person, they are moving far from each other and thus, won’t meet at this step. Otherwise, they will meet at the vertex having depth exactly in middle of both persons. We can easily find this vertex by lifting lower person to (d/2)th parent, if D is absolute difference in depths of both persons.
For this vertex to be meeting point at current step, two conditions have to be satisfied.
First is, that distance to be moved at current step is atleast D/2, otherwise both persons won’t reach any vertex of same depth at all.
Second condition is, the $D/2$th ancestor of the person moving up, say X, should lie on path of person moving down. To check this, we know the target for current step of person moving down. we can lift that target vertex to depth same as vertex X. This too can be done using binary lifting. If both vertices are same, persons meet at that vertex, hence answer increases by 1.
We can consider our previous example again.
Initial positions of both persons is 6 and 1 respectively. Absolute difference between depth is 4. Since person 1 is moving up, we can find (4/2) = 2nd ancestor of 6, That is, vertex 3. Now, we have to check two conditions mentioned above.
Distance covered at current step is 4, which is \geq D/2 since D = 4.
Also, depth of node 5 is 3 while depth of node 3 is 2. So, we need to find 3-2 = 1 ancestor of 5. We see, that it is also 3, hence both persons will meet at 3.
Both persons are moving in same direction at current step.
We know, that in this case, difference of depths of both persons never change. The reason is, depth of both of them either increase by 1 simultaneously, or decrease by 1. Hence, if starting vertices at current step are at different depth, we can see, they cannot meet in current step.
Here, There are two cases. Both persons are moving down, and both persons are moving up.
Both persons are moving up
If both persons at positions u and v respectively, we can see, that the first point they can meet is the LCA of (u, v). If the target vertex is lying below this LCA, there is no meeting point at this step. Otherwise, both persons reach the LCA at the same time, since their depth was same, and while reaching, it was reducing by 1 at every move.
The persons continue to meet till reaching their target vertex, which actually, will be same in this case. So, we have to count all vertices from LCA to the target vertex.
Consider the same tree, where first person has the path from 6 to 1, while second person has path from 7 to 1. they meet for first time at 3, then again at 2 and again at vertex 1. They meet actually at every vertex from LCA to target vertex. So, we can add depth[target]-depth[LCA]+1 to the answer.
Both persons are moving down
In this case, if the starting vertex of both of them is not same, it can be proven, that they cannot meet at current step. Beacuse as we move down a tree, we cannot reach the same node at same time, if we start from two different nodes.
Otherwise, we have starting vertex same for both persons. Now, they will continue to share meeting point till the LCA of their target location. We can similarly count number of vertices on part from start to this LCA and add to answer.
Important note for Implementation
- First thing, while splitting paths, we never move to next step for a person, till we complete current step.
- Second thing, we have to count vertices systematically. For example, at every step, i counted the vertices at every step, Including target vertex, but excluding start vertex, while tester included first vertex, while excluded last vertex.
I know, this implementation has a lot of edge cases which may lead to double-counting, so I’m commenting my solution, which you may refer below.
Time Complexity
Time complexity per step is O(logN), since we count meeting vertices using only LCA queries which can be handled by O(N*logN) preprocessing plus O(logN) query time, and there can be at most (K+L)*2 steps.
The overall time complexity is O(N*logN+(K+L)*logN) which is same as O((N+K+L)*logN).
Memory requirements is only the sparse table and the input vertices, which is same as O(N*logN+K+L).
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Editorialist’s solution (Commented)
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()