PROBLEM LINK:
Setter: Jafar Badour
Tester: Misha Chorniy
Editorialist: Taranpreet Singh
DIFFICULTY:
Hard
PREREQUISITES:
Computational Geometry and Integrals. Familiarity with Line-Sweep Algorithms would be helpful.
PROBLEM:
Given two projections of a body, one on XY plane having N vertices and other on XZ plane having M vertices, Find the maximal possible area of the body or determine if no such body exists.
QUICK EXPLANATION
- Any valid body shall exist if and only if minimum and maximum values of x coordinates of both projections coincide.
- We can consider the body as a number of extremely thin sheets merged together to form the body. By multiplying the area of such sheets by a corresponding thickness of sheets, we can compute the volume of such body.
- We can divide the body into parts by each x-coordinates of both polygons and use definite integration to compute the volume of the body between every two consecutive x-coordinates.
EXPLANATION
First of all, let us check whether any valid solid body exists or not, for the given two projections.
See, If we project the shadow of a body on the XY plane, it is nothing, but the hull of points formed by setting z coordinate as zero. Similarly, the shadow on the XZ plane is the hull of points formed by setting y-coordinate zero. (Note that hull here may be concave too, but surely not self-intersecting).
This way, the only thing we have is that we have x-coordinates preserved in both projections. The only check we have for a valid body is that both minimum x-coordinate and maximum x-coordinate should coincide for both polygons.
The reason is simple, If one polygon has a point with x coordinate smaller than the minimum of x-coordinates of the second polygon, It means, that the body has some solid part below minimum of x-coordinate of the second polygon, which cannot be true, as the second polygon is the projection of body on XZ plane. A similar argument holds for maximum x-coordinate too.
Thus, the two polygons become self-contradictory, if minimum and maximum values of x-coordinates of both polygons do not coincide.
Calculating maximal volume
Let us divide the body into thin sheets formed by taking x = c for all minX \leq c \leq maxX. We can see, that the volume of the body is just summation of the area of each sheet multiplied by its width.
Suppose, area of sheet at x is given by f(x). We can see that we need to find the maximal volume, and areas of sheets at different x are independent of each other. So, we want to maximize the area of each sheet too. The only way we can maximize the area of the sheet is when our body covers the whole area allowed by projections. Let g(c) be the length of projection at x = c on XY plane and h(c) be length of projection at x = c on XZ plane. It can be seen that f(x) = g(x)*h(x) where g(c) is the sum of length of line segments of line x = c strictly lying inside first polygon while h(c) is the sum of lengths of line segments of line x = c lying strictly inside second polygon.
Now, The problem here is, that we cannot run this process for each possible value of x. To help us, calculus comes to our rescue. We want to compute the sum of f(x) for all values in range [x1,x2], x1 \leq x2. It is a well-known problem and can be easily solved using definite integration, as follows.
Suppose we can write both g(x) and h(x) as linear functions of x. Say g(x) = a+b*x and h(x) = c+d*x. We get
\begin{equation} f(x) = (a+b*x)*(c+d*x) = (b*d)*x^2+(a*d+b*c)*x+a*c \end{equation}
Integrating both sides, we have
\int_{x1}^{x2} f(x) = \left | \frac{b*d*x^3}{3}+\frac{(a*d+b*c)*x^2}{2}+a*c*x \right |_{x1}^{x2} = F(x2)-F(x1)
where F(x) = \frac{b*d*x^3}{3}+\frac{(a*d+b*c)*x^2}{2}+a*c*x
Now, we divide the body into separate parts by planes, given by x = x_i for all distinct x_i present in either of the polygon. See the image below. Orange lines show partitioning polygon into parts for each distinct x coordinate.
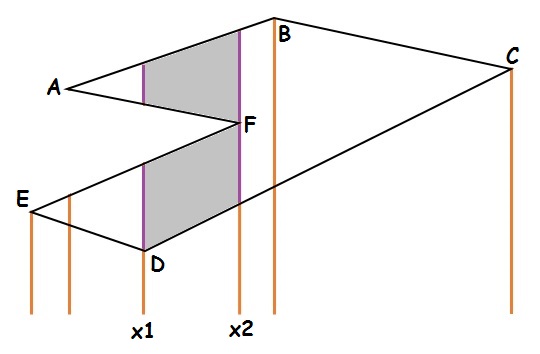
To represent the shaded area, we can add area below the line AB, subtract area below line AF, add area below line EF and subtract area below line DC, all in the range [x1,x2]. This can be achieved by just adding or subtracting equations of these lines, getting a linear function over x.
In the Image, for point x1, g(x1) is the sum of lengths of the two left purple segments while at x = x2, g(x) is the length of the purple segment at the right side. It can be seen, that if we try to draw line x = x3, x1 \leq x3 \leq x2, we shall obtain sum of lengths of segments lying inside polygon as g(x3-x1).
This can be generalized into three dimension by considering each distinct x out of all points and finding linear functions g(x) and h(x) which hold between each consecutive pair of x coordinate by adding a line into function when left end of the segment is to the left of x1 and removing it when its right end is also to the left of x1 for both polygons and calculating value of f(x) in range [x1, x2] using integration as explained above.
Adding or removing a line segment can be represented as operations over the slope and constant term when both line segment to be added, and the function g(x) are expressed in point-slope form.
Still in doubt? Refer to setter’s solution for details.
Learning Resources
- Computational Gemoetry basics
- Line Sweep Algorithms
- Area under the curve problem (in 2-dimension)
- Equations of a line
Time Complexity
Time complexity is O(N*logN+M*logM) per test case due to sorting.
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()