PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Sajal Agrawal
Tester: Xiuhan Wang
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Properties of triangles and Case-based Analysis.
PROBLEM:
Consider two Intersecting Lines interesecting at point A_0 having an angle \theta < 90° and marking N points A_1, A_2 \ldots A_N on lower line and B_1, B_2 \ldots B_N on upper line. Now join A_i with B_{i+1} and B_i with A_{i+1} for all 1 \leq i \leq N-1. Also join A_N and B_N.
Here, all these 2*N-1 are equal in length and are also equal to segments A_0A_1 and A_0B_1.
The problem requires to find out angle formed by two segments at a specific point. Queries are of four types. Given N, type and three integers x, y and z.
- Find angle A_xA_yB_z if the query is of the first type.
- Find angle A_xB_yA_z if the query is of the second type.
- Find angle A_xB_yB_z if the query is of the third type.
- Find angle B_xB_yB_z if the query is of the fourth type.
SUPER QUICK EXPLANATION
- For a given N, we can use Triangle sum property and Similarity of trinagles to systematically find out that \theta = \pi/(2*N+1). After this, \theta can be substituted to find the value of required angle.
- It can also be seen that the angles generated on both lines are following the same pattern. Specifically, Angles formed at point A_i are same as angles formed at point B_i. This way, answer to fourth query is exactly same as answer to second query, while answer to third query for triplet (x,y,z) is same as answer to first query for triplet (z,y,x).
- When y > 0, Angle A_{i-1}A_iB_{i-1} is \pi*(i-1)/(2*N+1) Angle B_{i-1}A_iB_{i+1} = \pi*(2*N+1-2*i)/(2*N+1) and Angle B_{i+1}A_iA_{i+1} = \pi*(i+1)/(2*N+1)
- Corner case when y = 0, answer is \theta = \pi/(2*N+1)
EXPLANATION
Ignore queries for now, first focus on determining the angle \theta between two lines.
Triangle properties used can be found below.
Click to view
- Sum of angles of a triangle is pi.
- Angles opposite to equal sides in a triangle are equal.
It can be seen that for a given N, Only one value of \theta is valid. Let us try to find this value for say, N = 4, as shown in the image below.
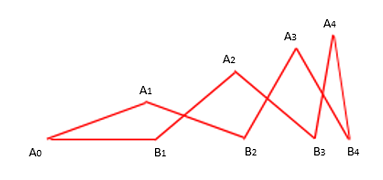
In \bigtriangleup A_0A_1B_2, \angle A_1A_0B_2 = \theta and we have |A_0A_1| = |A_1B_2| which implies \angle A_0B_2A_1 = \theta. Now, \angle A_0A_1B_2 = \pi-2*\theta which implies \angle A_2A_1B_2 = 2*\theta.
Consider \bigtriangleup A_1B_2A_3 now, where we have \angle A_2A_1B_2 = 2*\theta and |A_1B_2| = |A_3B_2|, implying \angle A_2A_3B_2 = 2*\theta. Applying Angle sum property, we have \angle A_1B_2A_3 = \pi-4*\theta. Now, \angle B_1B_2A_1 + \angle A_1B_2A_3 + \angle A_3B_2B_3 = \pi which implies \theta+(\pi-4*\theta)+\angle A_3B_2B_3 = \pi, giving \angle A_3B_2B_3 = 3*\theta. Once again we get \angle A_3B_4B_3 = \angle A_3B_2B_3 = 3*\theta.
Proceeding this way, we shall end up with \angle A_3A_4B_4 = 4*\theta and \angle A_3A_4B_3 = 3*\theta giving \angle B_3A_4B_4 = \theta. Also, we can find \angle A_4B_3B_4 = \angle A_4B_4B_3 = 4*\theta. Using angle sum property in \bigtriangleup B_3B_4A_4, we get \theta = \pi/(2*N+1).
Now that we have found \theta = \pi/(2*N+1), we can substitute this value to find out the answer for any query.
Corner case: Query 1 1 0 1 can be handled separately.
To answer queries, we need to notice the patter that A_{i-1}A_iB_{i-1} = \pi*(i-1)/(2*N+1) and B_{i-1}A_iB_{i+1} = \pi*(2*N+1-2*i)/(2*N+1) and B_{i+1}A_iA_{i+1} = \pi*(i+1)/(2*N+1). We can form case based analysis to answer queries of first type.
The answer to queries of second and fourth type is same due to symmetry and answer to such queries is \pi*(2*N+1-2*y)/(2*N+1).
It can be easily seen that answer to a query of the third type for triplet (x, y, z) is same as the answer to a query of the first type for triplet (z,y,x).
Time Complexity
Time complexity is O(1) per test case.
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Editorialist’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()
