PROBLEM LINK:
Author: Minako Kojima
Tester: Gerald Agapov
Editorialist: Jingbo Shang
DIFFICULTY:
Hard
PREREQUISITES:
Link Cut Tree, Heavy-Light Decomposition
PROBLEM:
Given a 0/1 colored tree of N nodes. Support two types operations (Q in total):
- Ask the size of same color connected component of node u;
- Toggle the color of node u.
EXPLANATION:
Both link cut tree and heavy-light decomposition can solve this problem. Here we mainly talk about the later one.
At the beginning, let me introduce the Heavy-Light Decomposition (HLD). The basic idea is to decompose the tree into some links consisting of heavy edges and some separate light links, as following (2 links only):
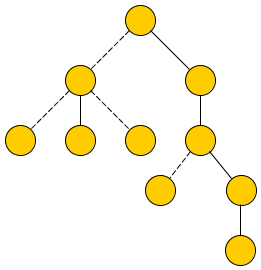
For each node, choose one of the biggest son as the heavy edge (choose anyone if there are some ties). This can ensure any path between two nodes in an N-node tree will pass O(logN) links. With this property, if we maintain a segment tree or any other balanced binary search tree on each link, a lot of queries can be dealt.
Suppose you have well known this data structure. Then, we try to apply HLD to this problem. First of all, let’s decompose the tree using HLD. Second, maintain the color and two values (the black/white sub-tree size rooted at this node assuming its color is black/white, despite what color it actually is) on each node u, denoted as Black[u] and White[u].
For each operation 1, starting from node u, we can upwardly find the lowest (with least depth, all nodes between them are same color) same color node and return the corresponding value stored.
For each operation 2, assume u is changed to black from white. Upwardly find the first black node, denote as v. Then, subtract White[u] from White[middle], middle are all nodes between u and v (not including u). After that, the similar things happened to black side again: upwardly find the first white node, denote as v, add Black[u] to Black[middle], middle are all nodes between u and v (not including u).
All steps introduced above can be supported by maintaining a Segment Tree on each links. For each operation, we can travel along different links upwardly and find the upmost same color node or the first different node. And for the subtraction/addition along the path, it could be done using the “segment cover” operation (with some values stored for the whole segment at segment tree nodes). Therefore, the time complexity can be controlled in O(Qlog^2N), here HLD contributes O(logN) and Segment Tree contributes for the other.
If you have questions about the segment tree’s operations, you’d better find some pure segment trees related problems and try to solve them. Because the key point of this problem is at HLD, we won’t discuss the segment tree detailly here.
AUTHOR’S AND TESTER’S SOLUTIONS:
Solutions to be uploaded soon.
Author’s solution can be found here.
Tester’s solution can be found [here][10].
[9]:
[10]: https://www.codechef.com/download/Solutions/2013/December/Tester1/QTREE6.cpp

