PROBLEM LINK:
Author: Tuan Anh Tran Dang
Tester: Gerald Agapov
Editorialist: Jingbo Shang
DIFFICULTY:
Hard
PREREQUISITES:
DFS order
PROBLEM:
Given an undirected simple graph with N nodes and M edges, find how many pairs of edges are fatal. A pair of edges are fatal if and only if the graph will be disconnected after we removed them.
EXPLANATION:
First of all, a trivial case is that, the given graph is disconnected. In such case, the answer should be M * (M - 1) / 2.
Therefore, we only concern the connected graph. Because of the connectivity, we can find a spanning tree first. Then, all edge can be classified into two sets: (1) Tree-Edge, (2) Non-Tree-Edge.
If we remove two Non-Tree-Edges, obviously, the graph will be still connected. If any Tree-Edge is removed, the connectivity depends on whether there are still some Non-Tree-Edges connect the two parts separated by this Tree-Edge in the spanning tree.
Let’s have a example as following (same as the sample input). Since the spanning tree can be chosen in any way, we choose the DFS-Tree starting from node 1 for the convenience (we will state the convenience later).
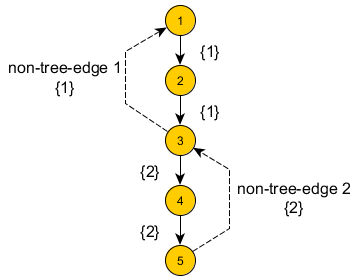
In this example, we can see that there are two Non-Tree-Edges (labeled as 1 and 2). And then, for each Tree-Edge, it is labeled by a set of Non-Tree-Edges which are crossing the edge. That is, if we delete that Tree-Edge, the Non-Tree-Edges in that set will connect the two separated parts. For a given Non-Tree-Edge, it will take care of a path on the DFS-Tree. Furthermore, in the DFS-Tree, there are only “children → ancestor” Non-Tree-Edges (i.e. back edges. This provides some conveniece).
Based on this label system, the forbidden pairs of edges are those edges with same label or some edge with empty set. For the first case, that is they depends on the same set of Non-Tree-Edges, after removing them together, the Non-Tree-Edges are not able to connect the three parts of tree (or the Non-Tree-Edge which is needed to connect the two parts are deleted). For the second case, edges with empty set as labels are all cuts, i.e. removing them will lead to disconnected state.
Therefore, our task is now focused on calculating the label of each edge. For a simple hash idea and the perfect (perfect because x xor x = 0) operation XOR, we can set a random number ranging from 1…2^64 - 1 to each Non-Tree-Edges. And then, represent a set of numbers as their XOR sum. That is, if a set is {1, 3}, the label will be treated as 2 (since 1 xor 3 = 2). Two sets are identical, if and only if their labels are same (high probability correct).
Finally, the only obstacle comes that how to XOR a number x to the edges between node u and v for all Non-Tree-Edges. And we need to query the XOR sum after all operations for all Tree-Edges. Thanks to the DFS-Tree we selected, without loss of generality, we suppose u is an ancestry of v. Denote prefix[u] as the XOR sum added to the path from root 1 to node u. Adding x to the path between u and v is equivalent to
prefix[u] = prefix[u] xor x;
prefix[v] = prefix[v] xor x
And after all Non-Tree-Edges are added to their corresponding paths on the DfS-Tree, we traverse the DFS-Tree again and can get the label on all Tree-Edges (it depends on the XOR sum of prefix[] in its sub-tree).
In the end, what we need is to count the number of pairs of labels, which are same or at least one zero. This could be done by hash too.
In summary, we have a O(N + M) algorithm to solve this problem with a high probability (due to the randomness to choose the Non-Tree-Edges’ labels). Because 2^64 is large enough comparing to the range of N and M, don’t worry about the probability. ![]() You will get AC if you implemented correctly.
You will get AC if you implemented correctly.
AUTHOR’S AND TESTER’S SOLUTIONS:
Author’s solution can be found here.
Tester’s solution can be found here.

