PROBLEM LINKS
Author: Abdullah Al Mahmud
Tester: Gerald Agapov
Editorialist: Praveen Reddy Vaka
DIFFICULTY:
medium-hard
PREREQUISITES:
Graph Theory, Maximum Independent Set in Bipartite Graphs, Max Flow/Min Cut, Geometry
EXPLANATION
Consider the following diagram as an example. The several polygons (there are four in total) represent the cuts made and the numbered regions denote the pieces formed as a result.
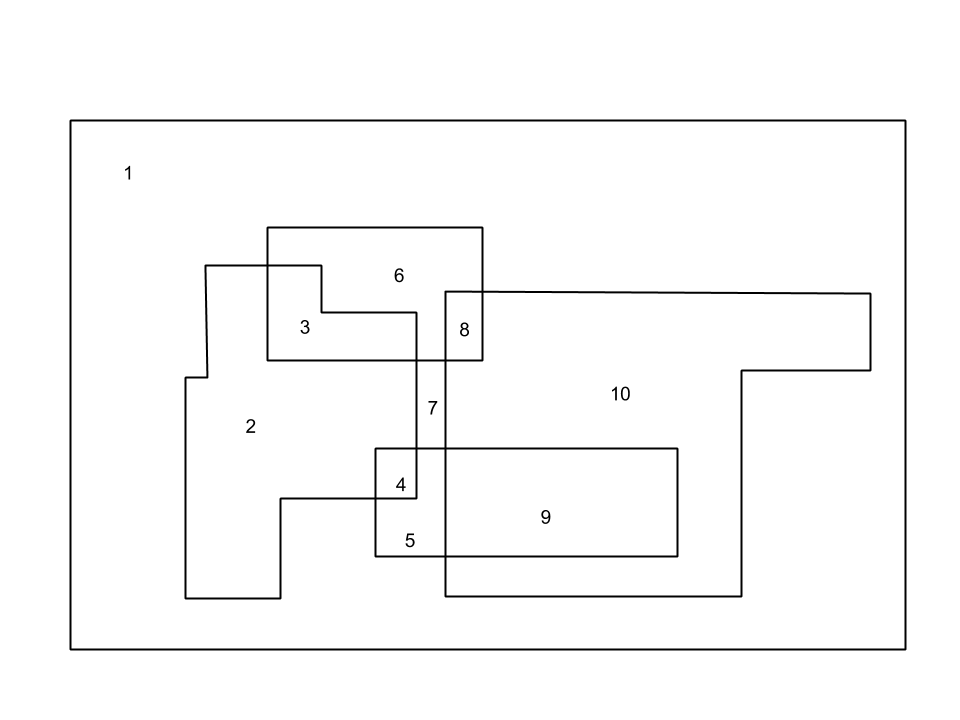
We can denote the cake as graph where each piece is a node and and two nodes will be connected if the corresponding pieces share an edge in the cake. In the original problem we have to choose cake pieces such that no two cake pieces have a side in common and the total volume of the cake pieces selected is maximum. If we denote the volume of each piece as a weight in the corresponding graph node. Our problem reduces to finding the set of nodes in the graph such that no two nodes are connected and the sum of weights is maximum. This is the maximum weighted independent set problem. This is a NP- Complete problem for general graphs but it can be solved in polynomial time for bipartite graphs. If we observe carefully the graph that we constructed will always be bipartite, due to the constraints placed on cuts (We will present a proof later). First let us see the graph representation of the cake shown above.

The complement of a independent set in a graph is a vertex cover. So the complement of maximum weighted independent set in a graph will be its minimum weighted vertex cover. We can construct a new graph G’ such that the the value of minimum weighted vertex cover in our graph will be same as the weight of minimum cut in G’. The construction is as follows. If our original graph is G and since G is bipartite we can divide the vertices into two sets R and B such all edges are between R and B only (we can use a simple dfs/ bfs to do this classification). Our G’ will be a edge weighted graph with all the vertices of G intact and all edges are given a weight of infinity. We add two new vertices source and sink. for every i in R we add an edge from source to i with a weight oght of area(i). for every j in B we add an edge from j to sink with a weight of area(j). Minimum vertex cover in the original graph is same as minimum cut in G’ which we can find using max flow. The answer will be (total area - obtained value for min cut).
SOLUTIONS
Setter’s Solution: CAKE2AM.cpp
Tester’s Solution: CAKE2AM.cpp