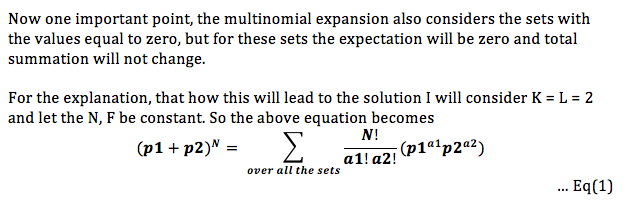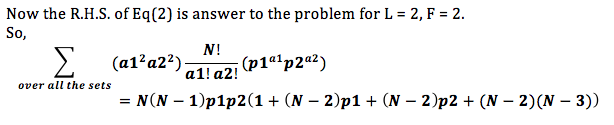PROBLEM LINK:
Author: Pavel Sheftelevich
Tester: Mugurel Ionut Andreica
Editorialist: Lalit Kundu
DIFFICULTY:
Hard
PREREQUISITES:
combinatorics, advanced mathematics, fft
PROBLEM:
Suppose you have a dice with K faces with numbers from 1 to K written on it, and integers L and F(0 \lt L \le K). You roll it N times. Let a_i be the number of times(out of the N rolls) that a face with number i written on it came up as the top face of the dice. Find the mathematical expectation of the value a_1^F * a_2^F * ... * a_L^F.
QUICK EXPLANATION:
================
Write a_i as x_{i, 1} + x_{i, 2} + ... x_{i, N}, where x_{i, j} is 0 or 1 depending on whether we got the value i on the j^{th} dice roll. We can write probability of x_{i, j} being 1 as \frac{1}{K} as we can get any value from 1 to K equally probably in the j^{th} roll of dice.
For F=1, our answer will be number of terms of form x_{1, A_1} * x_{2, A_2} * ... * x_{L, A_L} where all A_i are distinct, divided by K^L. Number of such terms is \binom{N}{L} * L!.
For F>1, for each polynomial of form (x_{1, 1} + x_{1, 2} + ... x_{1, N})^F first we individually define \textrm{num_ways}[F, i] as number of ways to choose F variables f_1, f_2 ... f_F such that 1 \le f_j \le i and and atleast one of the f_j is i. Then, we traverse over number of terms P from L to L*F and for each P we add to answer \frac{\textrm{num}}{\textrm{den}} where \textrm{num} = \binom{N}{P} * P! * n_P and \textrm{den} = K^P; where n_p can be written as
coefficient of x^P in polynomial (\textrm{num_ways}[F, 0]x^0 + \textrm{num_ways}[F, 1]x^1 + \textrm{num_ways}[F, 2]x^2 + ... + \textrm{num_ways}[F, F]x^F)^L.
EXPLANATION:
================
Warning
I personally found it a very complex mathematical problem, but I am not a pure maths guy, so it is fine. Now, if you really want to understand this and you are not a math guy, you’ll need to put down your utmost attention to the detail in this editorial.
Now, let us move to solving the problem.
First a very basic definition of the expected value E[X]. Suppose random variable X can take value x_1 with probability p_1, value x_2 with probability p_2, and so on, up to value x_k with probability p_k. Then the expectation of this random variable X, E[X] is defined as x_1p_1 + x_2p_2 + ... + x_kp_k.
The first most basic observation is that we can’t directly deal with variables a_i, we need to break them down into smaller components. The most easy way to deal with them would be to write a_i as x_{i, 1} + x_{i, 2} + ... x_{i, N}, where x_{i, j} is 0 or 1 depending on whether we got the value i on the j^{th} dice roll. We can write probability of x_{i, j} being 1 as \frac{1}{K} as we can get any value from 1 to K equally probably in the j^{th} roll of dice.
F=1
First, let’s solve for the case where F=1. We are interested in
E[(x_{1, 1} + x_{1, 2} + ... x_{1, N})*(x_{2, 1} + x_{2, 2} + ... x_{2, N})* ... *(x_{L, 1} + x_{L, 2} + ... x_{L, N})].
Now, this polynomial inside can be expanded to get various terms of the form x_{1, A_1} * x_{2, A_2} * ... * x_{L, A_L} where 1 \le A_i \le N. Our expected value is sum of expected value of all these terms. Now, all these terms x_{i, A_i} should be 1 for this certain value to contribute to the expected value. Now, thing worth noting here is that if in a particular term for any p and q such that 1 \le p \ne q \le L and A_p = A_q, the expected value of this term is zero because probability of such an event is zero. For example, for a term like x_{1, 2} * x_{2, 2} * ..., the probability of this term is zero because this the term is stating that we got value 1 in 2^{nd} dice roll and we also got value 2 in 2^{nd} dice roll which is not possible.
So, we are only interested in terms where all A_i are distinct. Probability of each such term to be 1 is \frac{1}{K^L}, because we need each term to be 1. So, if there are n variables of form x_{1, A_1} * x_{2, A_2} * ... * x_{L, A_L} where all A_i are distinct, our answer is \frac{n}{K^L}(this follows from the definition of expectation). Let’s see what is value of n. We are trying to get L distinct values out of N values, which is basically \binom{N}{L} and note that order also matters here, so n = \binom{N}{L} * L!, where \binom{n}{k} = \frac{n!}{k!(n-k)!} is number of ways to select k distinct objects out of n distinct objects and n! = 1*2*...*n.
So, we say here that our numerator is \frac{N!}{(N-L)!}, where N \le 10^9 and L \le 50,000. We can write this as (N-L+1) * (N-L+2) * ... * (N), whih can be calculated in O(L). We can easily calculate denominator i.e K^L here using modular exponention. For inverse modulo, since modulo is prime we can use Fermat’s Theorem.
F > 1
Before dwelling deep into the solution, I’d tell here an interesting result which we’ll be using ahead. Understanding this is important before going into the solution. Let’s say there are variables x_1, x_2 ... x_N which are non-negative integers. For assigning an integer x to a variable x_i, there are f(x) number of ways to do it. Now, we want to calculate total number of ways to choose integers x_1, x_2 ... x_N such that x_i \ge 0 are integers and x_1 + x_2 + ... + x_N = M. So, here we need to consider each integral solution of type y_1, y_2, ... y_N, such that y_1 + y_2 + ... + y_N = N, and for each such integral solution add to answer f(y_1) * f(y_2) * ... * f(y_N).
I won’t derive the result here; total number of ways in this case are coefficient of x^M in polynomial (f(0)x^0 + f(1)x^1 + f(2)x^2 + ... f(M)x^{M})^N. You can read more about use of generating functions in combinatorics here.
Now, this is where it gets interesting. Here we are interested in
E[(x_{1, 1} + x_{1, 2} + ... x_{1, N})^F * (x_{2, 1} + x_{2, 2} + ... x_{2, N})^F * ... *(x_{L, 1} + x_{L, 2} + ... x_{L, N})^F].
Now, what is different from F=1? In the earlier case, there were L variables in each term, but now we can have P variables where P ranges from L to L*F. For example, this is a term with L*F variables
x_{1, A_1} * x_{1, A_2} * ... * x_{1, A_F} *
x_{2, B_1} * x_{2, B_2} * ... * x_{2, B_F} *
.
.
.
x_{L, Z_1} * x_{L, Z_2} * ... * x_{L, Z_F}.
where 1 \le A_i, B_i, ... Z_i \le N.
And the observation is that if for any i, j such that 1 \le i \le j \le F, A_i = B_j or A_i = C_j or … or A_i = Z_j and similarly for B and C and so on, that particular term won’t contribute anything to answer by the same logic as we had in case of F=1. However, any A_i could be equal to A_j as it just denotes that 1 came in A_i roll as well as A_j roll of the dice.
So, what is our approach going to be? For each P from L to L*F, we’ll calculate number of terms with P variables. Say, if number of such terms is n_P, then we add to our answer \frac{\textrm{num}}{\textrm{den}} where \textrm{num} = \binom{N}{P} * P! * n_P and \textrm{den} = K^P by the same logic as we had in F=1.
Now, let’s see how to calculate n_P. First we should remember what n_P is. It is number of terms in expansion of our overall polynomial such that there are P variables in those terms.
There are L individual polynomials (x_{1, 1} + x_{1, 2} + ... x_{1, N})^F, (x_{2, 1} + x_{2, 2} + ... x_{2, N})^F and so on till (x_{L, 1} + x_{L, 2} + ... x_{L, N})^F that we are interested in. We’ll try to process each polynomial individually.
Let’s say W_i denotes the number of variables the i^{th} polynomial of the total L polynomials contribute. We want to calculate number of ways such that W_1 + W_2 + ... + W_L = P where W_i \ge 0. But, for each value \ge 0 we give to any variable W_i, there are some number of ways attached with it too. For example, if we give W_1 a value of 1, then we also have to multiply number of ways to choose 1 distinct value x(1 \le x \le N) such that A_1 = A_2 = ... A_F = x, or if we give a value of 2 to W_2, then we have to choose B_1, B_2 ... B_F from 1 to N in such a way that only 2 distinct values occur in these.
Now, another interesting thing is that number of ways to choose i distinct values of 1 to N doesn’t depend on whether we are choosing those values for W_1 or W_2 and so on. So, if we define a new term here \textrm{num_ways}[F, i] as number of ways to choose F variables f_1, f_2 ... f_F such that 1 \le f_j \le i and atleast one of the f_j is i, then n_p can be written as
coefficient of x^P in polynomial (\textrm{num_ways}[F, 0]x^0 + \textrm{num_ways}[F, 1]x^1 + \textrm{num_ways}[F, 2]x^2 + ... + \textrm{num_ways}[F, F]x^F)^L.
This follows from the result written at starting of this section. Let’s assume that we have calculated \textrm{num_ways}[F, i] for all 0 \le i \le F, then how do we proceed?
Note that our P ranges from L to L*F, so enumerating the whole polynomial
(\textrm{num_ways}[F, 0]x^0 + \textrm{num_ways}[F, 1]x^1 + \textrm{num_ways}[F, 2]x^2 + ... + \textrm{num_ways}[F, F]x^F)^L
is a good option. Now, raising polynomials to power can be done is same way as we raise integers to power via fast exponentiation. However, to quickly multiply two polynomials we’ll use FFT. Using FFT we can multiply two polynomials of degree N in N \textrm{log}N. So, our total complexity of evaluating that polynomial would be complexity of multiplying two polynomials of degree atmost L*F atmost O(\textrm{log} L) times(due to fast exponentiation). So, total complexity would be O(L * F * \textrm{log}(L * F) * \textrm{log} L) which can written as O(L * F * \textrm{log}(L * F).
But, but, there is an other interesting observation to avoid all this computation. Note that we multiply n_p with \binom{N}{P} * P! in numerator and divide by K^P while adding to answer. But, our answer is modulo 2003, so, for P > 2003, \binom{N}{P} * P! is guaranteed to be zero (because it is the product of at least 2003 coefficients, one of which is certainly dvisible by 2003). So, we never need more than the first 2003 coefficients of the final polynomials.
Now, the part that we have left to understand is how to calculate \textrm{num_ways}[F, i] for 1 \le i \le F. To revise, \textrm{num_ways}[F, i] is number of ways to choose F variables f_1, f_2 ... f_F such that 1 \le f_j \le i and and atleast one of the f_j is i. We can easily define a recurrence \textrm{num_ways}[F, i] = \textrm{num_ways}[F-1, i-1] + i*\textrm{num_ways}_[F-1, i].
How do we arrive at this reccurence?
The first term indicates the case that the value i value occurs only once on f_1, f_2, ..., f_F, so we add number of ways to choose i-1 values for F-1 values and second term denotes the case that value i has occured earlier, therefore it can have any of the 1, 2, ... i already existing values. So, we multiply \textrm{num_ways}_[F-1, i] with i and add to answer. Incidentally, these numbers are Stirling numbers of second kind. So, we can calculate all required values in O(F^2) here.
PROBLEMS TO SOLVE
===================
CNTDSETS
DEVLOCK
TASUMOBC
FARASA