Let’s say I have n pairs of integers (not necessarily positive. The ith line consists of a pair of numbers ai and bi.
What is the quickest way to find if (bj - bi) / (ai - aj) lies within a certain range? I can only think of the usual O(N^2) solution but a solution of lesser time complexity?
I am trying to solve Anton and Lines from Round 329 on Codeforces.
Problem link: Problem - B - Codeforces
1 Like
NOTE : I found this on a codeforces blog and I thought it would help you. It was written by DollarAkshay so all credits goes to him.
If you try a brute force method of checking each pair you wont pass because its a O(n^2) algorithm. Instead of lines think of them as line segments from X1 to X2 You have to find the y intercepts at X1 and X2. Create a pair vector of the form { line_number , X1_Y_intercept} Create another pair vector of the form { line_number , X2_Y_intercept} Sort them both based on X1_Y_intercept and X2_Y_intercept." Now if the ordering of the line_number is the same in both vectors then there is no intersection else there is an intersection
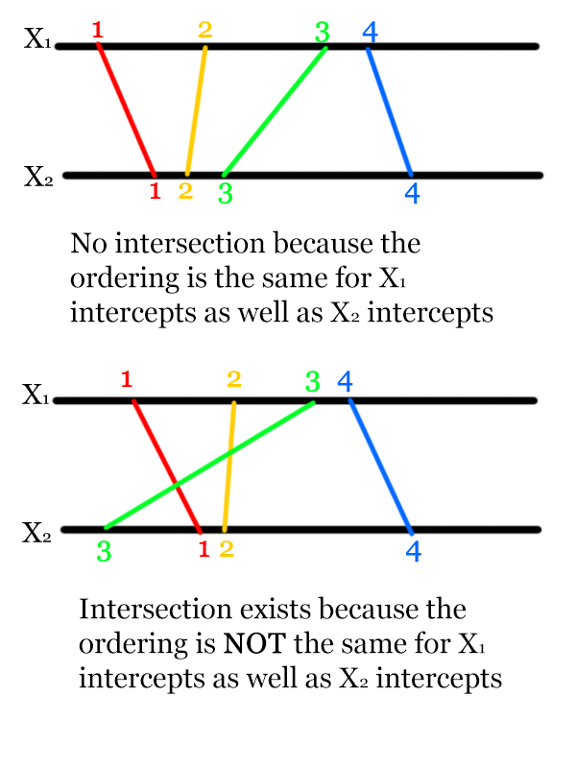
2 Likes
Here is my ACed solution in java Submission #14078868 - Codeforces
Ahhh, I never thought of them geometrically as line segments, merely solutions of the line equations. Thanks!
btw, regarding my first question, is there no way out?
Sorry I can’t understand your problem , can you be more precise.
