PROBLEM LINK:
Author: Vasia Antoniuk
Tester: Istvan Nagy
Editorialist: Miguel Oliveira
DIFFICULTY:
Easy
PREREQUISITES:
Combinatorics
PROBLEM:
Given an array A of N integers, a position x, and a number M, find the value of A_x after performing the following operation M times:
for i = 2 to N:
A[i] = A[i] + A[i-1]
As the answer could be large, the answer should be given modulo 1\,000\,000\,007.
EXPLANATION:
Subtask1
In the first subtask, we have x \leq 2. So we only have 2 cases:
- x = 1: A_1 is never changed in the given procedure, so we already have the result (don’t forget the modulo!)
- x = 2: in each execution of the above procedure, we add A_1 once to A_2. So the result is just A_2 + M \times A_1.
Subtask 2
The second subtask guarantees that N \times M \leq 10^6. This means that we can just perform the given algorithm M times. This approach takes O(N\times M) time, which is ok with these constraints.
Subtask 3
The number N is irrelevant if larger than x because A_x is only affected by indices smaller than x. Hence, I will consider N=x for the rest of the editorial, i.e., we will want to know the value of A_N.
When we are given a set of operations to be performed, a good starting point is to see what happens after a few iterations. Suppose we have N = 5, and the initial values are A_1 = a, A_2 = b, A_3 = c, A_4 = d, and A_5 = e.
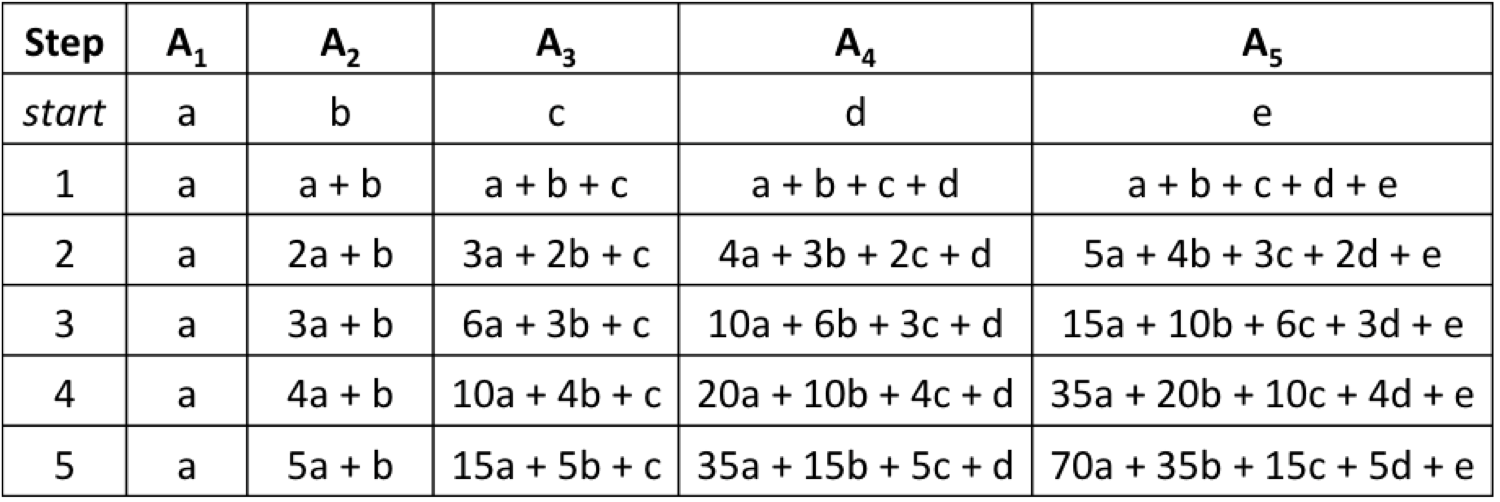
You may recognise that the factors associated with each initial value are binomial coefficients.
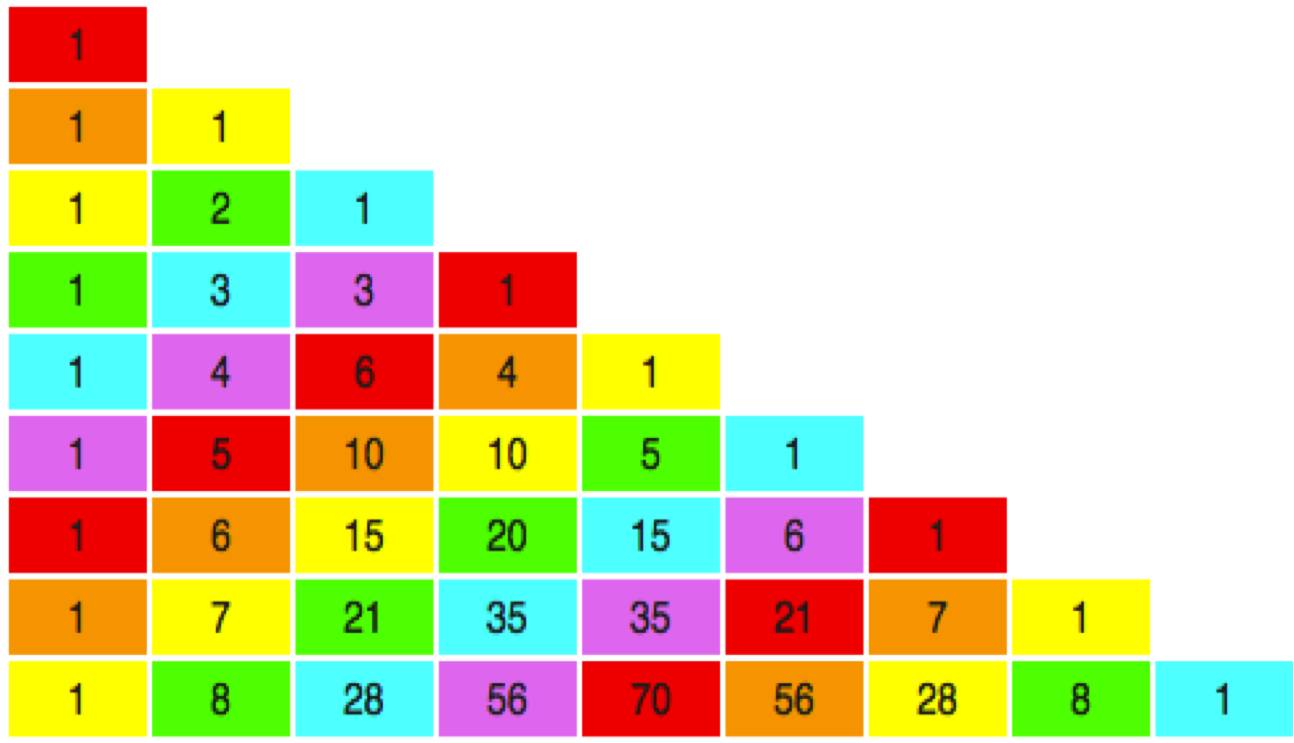
In each step, we are summing the values of a column in the Pascal Triangle. In the above example, M= 5, so we are interested in summing the first 5 lines in each column. For example, the value associated with a in the final A_5 is the result of \binom{3}{3} + \binom{4}{3} + \binom{5}{3} + \binom{6}{3} + \binom{7}{3}.
It can be shown (see here) that \sum_{m=0}^n{\binom{m}{k}} = \binom{n+1}{k+1}. In fact, \sum_{m=0}^7{\binom{m}{3}} = \binom{8}{4} = 70.
So, we now have a formula to get the coefficient of each initial value, in order to get the final A_N. In the above example, we have A_5 = \binom{M+3}{4} a + \binom{M+2}{3} b + \binom{M+1}{2} c + \binom{M}{1} d + \binom{M-1}{0} e = \\ \binom{8}{4} a + \binom{7}{3} b + \binom{6}{2} c + \binom{5}{1} d + \binom{4}{0} e = \\ 70a + 35b + 15c + 5d + e
The binomial coefficient can be calculated as \binom{n}{k} = \frac{n!}{k! (n-k)!}. M is up to 10^{18} so it is too big to calculate the factorial directly. However, we can take advantage of the formula we are calculating.
\binom{M+3}{4} = \frac{(M+3)!}{4! (M+3-4)!} = \frac{(M+3)!}{4! (M-1)!} = \frac{M * (M+1) * (M+2) * (M+3)}{4!}
\binom{M+2}{3} = \frac{M * (M+1) * (M+2)}{3!}
\binom{M+1}{2} = \frac{M * (M+1)}{2!}
\binom{M}{1} = \frac{M}{1!}
\binom{M-1}{0} = 1
As you can see, we can calculate each factor iteratively using the previous value. In order to divide by each factorial, we need to use the Modular Multiplicative Inverse, which can be computed in O(\log{N}). So, the time complexity of this approach is O(N \log{N}).