PROBLEM LINK:
Authors: Jaub Safin
Testers: Vasya Antoniuk
Translators: Vasya Antoniuk (Russian), Team VNOI (Vietnamese) and Hu Zecong (Mandarin)
Editorialist: Praveen Dhinwa
DIFFICULTY:
Medium
PREREQUISITES:
edge cover, bit compression, bit mask dp
PROBLEM:
You are given an undirected graph G with N vertices and M edges. A cycle of length three is called a triangle.
Find out the minimum (possible zero) number of vertices you should remove from G such that remaining graph does not contain any triangle.
You are also given that there can be at max 40 triangles and each vertex belongs to at most 2 triangles. N can be at most 3000.
QUICK EXPLANATION:
Find all the triangles of graph G by maintaining a bit compression vector for denoting neighbours of a vertex.
Construct a graph G' consisting of T vertices, where each vertex corresponds to a triangle. Two vertices have an edge between them iff their corresponding triangles have at least one vertex common.
Now our problem reduces to the problem of finding minimum edge cover of the graph G'.
Finding minimum edge cover of a graph can be done in \mathcal{O}(T^{\frac{3}{2}}) time using general maximum matching algorithm as a subroutine.
The expected solution was a bitmask dp. We iterate over vertices in suitable order and remember minimum number of edges necessary to cover already proecessed vertices. We choose all possible ways of selecting next vertex to process and update the dp. This is too slow to pass.
You can optimize this dp by choosing a suitable order of vertices to process. At each step, the next vertex to process will be the one which is incident to the earliest possible already processed vertex. We will drop a vertex from our state if all of it’s neighbour vertices have been processed. This way, we will be maintaing only set of some “interesting” vertices in our dp state, i.e. the vertices whose some neighbour vertex is not yet processed. One can note that size of set of “interesting” vertices can be at max \frac{T + 3}{2} vertices at a time. By using this observation, we can optimize this dp to run in \mathcal{O}(T^2 2^{\frac{T}{2}}) time.
EXPLANATION:
Find all triangles
First let us identify all the triangles in the given graph. The trivial idea would be to enumerate over all possible triplets of vertices and checking whether they form a triangle or not. Unfortunately, it won’t run in time for N = 3000 as it takes \mathcal{O}(N^3) time.
Formally, we can implement the above method by maintaining an array neigh_u of size N for each vertex u, where neigh_u[i] is a binary number denoting whether vertex i is a neighbour of u or not. After that we iterate over each edge (u, v) in the graph G and find all vertices w such that both neigh_u[w] and neigh_v[w] are 1.
Note that the array neigh_u is binary array. So, we would like to make use of bitwise operations to speed up the calculation of finding all possible w's. We can compress the neigh_u array by a factor of B by using B-bit integers. Now the size of neigh_u array will be \lceil N/B \rceil.
Now, to find all possible w's for each edge (u, v), we will construct an array AND such that AND[i] = neigh_u[i] & neigh_v[i] for each i, where & denotes bitwise and operation. Note that there won’t be more than 2 set bits in the entire array AND, otherwise the condition of each vertex being adjacent on at most two triangles will be violated. So, the most values of the array AND will be zeros. There can be atmost 2 non-zero entries in AND array.
So, we used \mathcal{O}(\frac{N}{B}) space for each vertex u. Total space used will be \mathcal{O}(\frac{N^2}{B}).
For each edge in the graph G, we take \mathcal{O}(\frac{N}{B}) time to compute common vertices. Hence total time taken is \mathcal{O}(\frac{N * M}{B}) where M factor is due to maximum possible number of edges (can go upto to \mathcal{O}(N^2)).
We can choose B to 32 or 64 to make sure that both space and time complexity fit in the desired limits.
Reduction to Edge Cover problem
Construct another graph made only of triangles
Now, let us create another graph G' consisting of T vertices, each corresponding to a triangle in the graph G. There will be an edge between two vertices u and v in G', if there is a common vertex in triangles corersponding to u and v. Note that maximum degree of G' can be at most 3.
Now, the answer of our problem will be equal to minimum edge cover in the graph G'. Edge cover of a graph is a subset of edges such that each vertex is incident on at least one of the edges in the subset. This problem can be solved in polynomial time by finding a maximum matching the graph. All the edges of maximum matching will be part of our edge cover. Other than those, we will select the necessary edges to cover yet uncovered vertices that are still not covered greedily. Please see the following link for more details.
Bitmask dp solution
But implementing maximum matching algorithm for general graphs can be quite tedious unless you have it in your library.
Our intended solution was a bitmask dp solution which is much easier to implement.
The dp consists of processing the vertices in suitable order and remembering the minimum number of edges necessary to cover some subset of already processed vertices. Let dp[mask] denote the minimum number of edges needed to cover vertices represented by bitmask mask. Transitions of this dp can be done by trying each possible unprocessed vertex incident on the set of already processed vertices. This leads to a time complexity with exponential factor being \mathcal{O}(2^T) which won’t fit in time as T can be at max 40.
Speeding up the dp
The key to speeding up this dp lies in choosing a suitable order for processing the vertices. We start with any vertex. At each step, the next vertex to process will be the one which is incident to the earliest possible already processed vertex.
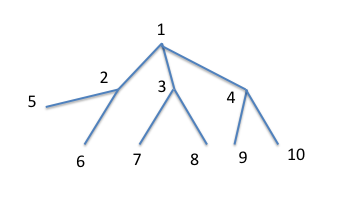
Let us see an example. Let G' be the above given graph.
Assume that we start from vertex 1.
The next vertex to process will be one of {2, 3, 4}. Assume that we select 2. Then the next vertex to process can be {3, 4}.
Assume we selected 3, then the next vertex to process would be 4.
Now, after that note that we have taken care of all the edges incident from vertex 1. So, we don’t even need to maintain 1 in our dp state.
So, our dp state at this point will maintain {2, 3, 4} only.
Hence the number of processed vertices to maintain in the state follow the sequence 1 (included 1), 2 (included 2), 3 (included 3), 3 (we included 4 and dropped 1).
That way, the number of processed vertices incident on some not yet processed one is bounded by the sequence 1,2,3,3 (we just processed all ≤ 3 neighbours of the vertex processed first, so we added one vertex, but stopped counting the first one), 4, 4 (we stopped counting the second processed vertex), 5, 5, etc. We can see that the k-th member of this sequence is at most (k + 3)/2; for a graph with less vertices of degree 3 or multiple connected components, it’s even less.
Herein lies an exponential factor of 2^{\frac{T}{2}} in the time complexity - if we call the vertices incident on a not yet processed verte “interesting”, we can only do the DP on states given by subsets of interesting vertices. For example, in the above case we dropped 1 from the set of interesting vertices when each of its neighbours were processed. After processing a vertex, we’ll find all vertices which stopped being interesting and purge the states in which they aren’t covered yet.
The number of states is now \mathcal{O}(2^{\frac{(T +3)}{2}}), so the DP takes \mathcal{O}(T \, 2^3 \, 2^{\frac{(T +3)}{2}}) = \mathcal{O}(2^{\frac{(T + 9)}{2}}) time and finding the states to purge takes \mathcal{O}(T \, 2^{\frac{(T+3)}{2})}) per vertex. Note that 2^3 factor is due to considering any of the three neighbours of earliest processed vertex as next candidate vertex to process.
Hence this part has time complexity \mathcal{O}(T^2 2^{\frac{T}{2}}).
Time Complexity:
As explained above, time complexity of dp \mathcal{O}(T^2 2^{\frac{T}{2}}) and time complexity of computing all triangles will be \mathcal{O}(\frac{NM}{B}). So time compexity of the entire program will be \mathcal{O}(\frac{NM}{B} + T^2 2^{\frac{T}{2}}) per test case.