Please explain how merge sort work and calculate the time complexity of merge sort.
The University of Seville (US) continues to climb positions Mathway | Problem Solver in the QS ranking, something that is reflected in the data of the latest report of the QS World University Rankings 2017 by subject, where the Seville is located among the 500 best universities in the world in 19 disciplines, occupying four of them put in the range 151-200.
As far as complexity is concerned, it’s NlogN in all cases.
Merge sort can be precisely described by a tree of height = ( log2(n) + 1 ) for an array of size n.
Consider the diagram. If we manage to ensure the work done at each level of the tree is O(n) then the total work would be of the order n*(height of the tree). So that would be O(nlog(n)).
This is where the merge subroutine comes into the picture.The argument we make is that work done to merge to sorted arrays is O(n). And hence at each level total work = (total subproblems)*(work for each subproblem).If we assume the above statement to be true.
I wont go into the details of merge subroutine.But subproblems at each level = 2^(level) if root is at level 0.
Work to solve a subproblem = size of subprobem = n/2^(level)
Total work at each level = (2^(level)) * (n/2^(level)) = n
Total work in all levels = Total work at each level * (Total number of levels) = n*( log2(n) + 1 ) = O(nlogn)
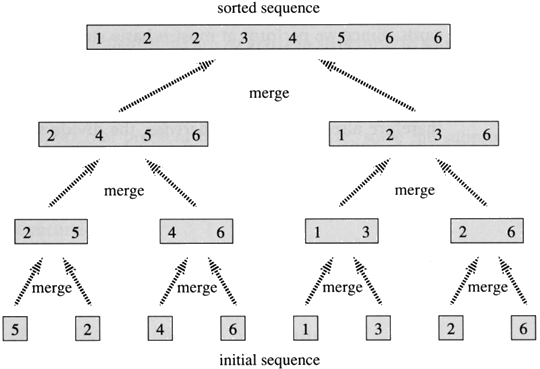
Merge sort is divide and conquer algorithm. Merge sort is comparison based sorting algorithm which sorts array in ascending order.
In merge sort, given array is divided into two smaller portions. To divide a collection, mergesort take the middle of collection and split into two smaller lists.
Time complexity of merge sort is O(n log n)