Overview:
Stack is data structure where elements is inserted at the top of the list and any element is deleted from the top of list. So it is called LIFO data structure. Insert operation on a stack is often called push and delete operation is often called pop.
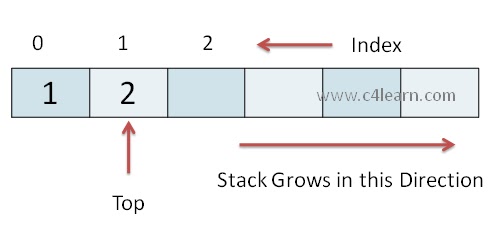
The following picture top is an indicator that indicates the top element of the stack.
Real life applications of stack:
There are many real life example of stack. In our daily life, we see stack of plates in cafeteria or restaurant, stack of the books in book shop.
The palate which is at the top is the first one to deleted. Similarly the plate which is at the bottom most is the last one to be deleted.
Operation :
**The following operation are performed in the stack.
- Push : To add an element to a stack.
2.Pop : To remove an element from the stack.
3.Peek : To get the topmost element.**
Implementation :
Stack can be implemented two ways. using array and using linked list.Here we discuss stack implementation using array.
The stack which is implemented using array array is called array based stack. It uses top variable to print the top most element in the linear array.
1. Initially top=0
2. In Push operation top is increased by one and pushed item to stack[top]
3. In Pop operation top decrease.
4. In Peek operation check that the top is not zero and return stack[top].
Algorithm : Push(stk, n, item)
Step 1: Start
Step 2: if(top==n) print overflow
else stk[top++]=item.
Step 3: End
C++ implementation : void push(int stk[],int n, int item) { if(top==n) cout<<"Overflow"<<endl; else stk[top++] = item; }
Algorithm : Pop(stk)
Step 1: Start
Step 2: if(top==NULL) print Underflow;
else top--;
Step 3: End
C++ implementation : void pop(int stk[] ) { if(top==NULL) cout<<"Underflow"<<endl; else top-- ; }
Algorithm : Peek(stk)
Step 1: Start
Step 2: if(top==NULL) print Underflow;
else return stk[top-1];
Step 3: End
C++ implementation : int peek(int stk[] ) { if(top==NULL) cout<<"Underflow"<<endl; else return skt[top-1]; }
Stack has many application . We can convert an infix into post-fix expression using stack. We can explain this.
We start to scan the expression from left to right. In an expression , there may be some operands, operators and parenthesis.
Steps:
1. If a symbol is an operand add it to the post-fix expression.
2. If the symbol is an opening parenthesis push it on the stack.
3. If the symbol is an operator.Then check the top of the stack.
(i) If the precedence of the operator at the top is higher or same as the current operator then repeatedly it is popped and added to the post-fix expression.
(ii) Else it pushed onto the stack.
4.If the symbol a closing parenthesis then
(i) Repeatedly pop from the stack and add each operator to the postfix expression until the corresponding opening encountered.
(ii) Remove the opening parenthesis from the stack.
C++ implementation : void prefex2postfix(string s) { stack<char>st; for(int i=0; i<s.length(); i++) { if(isdigit(s[i]) || isalpha(s[i])) cout<<s[i]; else if( s[i]==')' ) { while(st.top()!='(') { cout<<st.top(); st.pop(); } st.pop(); } else st.push(s[i]); } }
Stack full source code : link
Codechef Problem : ONP , BEX
Spoj Problem STPAR , Transform the Expression
Hackerrank : Balanced Brackets