CHEFYODA solution

[bansal1232]

This question is simple as it looks! The Matrix N * M is been given to check your presence of mind! If you give attention for few minutes then you wil find that-

• If N and M will be odd then answer
  will be 0 (Chef can not win the
  game).
• if N and M both will even then answer is 1 as chef
  will always will the game whatever set he will choose.
• The main problem will occur when
  Matrix size is not both even or odd.
  Means when only one of them is even
  or odd in value of N and M.

So how to solve this part! It simple as you will see chef will win only in first set of rule. So by using combinatorics you will find that the answer will be given as ∑(i=p to i=k) (^kC_i / 2^k ) i.e, (^kC_i + ^kC_i+1 + … + ^kC_k )/ 2^k.

Now the question boils down how to find such value for the range upto 10⁶ ?

So here we will use the logarithm approach to avoid overflow and store all these value in dp[] array like… n! = n * (n-1) * (n-2) * (n-3) * … * 3 * 2 * 1. As we will store the factorial of n by taking log2() on both sides as log(n!) = log(n) + log(n-1) + log(n-2) + … + log(3) + log(2) + log(1).

Now when we need factorial of any number then we just use this precomputed value. How?

Suppose if we wanna find the value of ^kC_i then we can write it as dp[k] - dp[k-i] - dp[i]. but we have extra factor of k from 2^k so we will subtract it from this value. and the result will become as res= dp[k] - dp[k-i] - dp[i] - k. Now this result is in log₂() form so to get actual value we will convert to result as 2^res

for(i=p;i<=k;++i)
   {
    res=dp[k]-dp[i]-dp[k-i]-k;
    ans+=pow(2.0, res);
 
   }

Tada! Now your question has been solved!

Just see my solution part to know more about how it is working. Click

If anyone have still query then please feel free to ask.

[avi892nash]

The answer to the solution is cumulative sum binomial distribution. So you can calculate nC(r+1) from nCr from simple math calculation. You can store answer in long double but if it becomes greater then some limit like e.g 1000 then divide it by 2 until it become less than 1. Here is my solution AC in 0.19 seconds CodeChef: Practical coding for everyone

[bhishma]

I got the logic that when chef wins in exactly one of the strategies we need to find the cumulative binomial probability . But I am facing some issue in the logic to find whether chef has a winning strategy for a given board dimension.

When I am at coordinate (i,j) and turn t (1 (chef) , 0 (yoda)) , I mark that coordinate and If current turn is chef then either one of the adjacent move should lead to a optimal game or else I loose . If the current turn is yoda then all adjacent move he takes chef should win or else yoda will take that move and chef will lose .

My Code : https://www.codechef.com/viewsolution/12806209

Can someone help me in finding my mistake.

[aditya211935]

We can also use incomplete beta function for computing cumulative binomial distribution. The winner of the contest used it.
You can read more about this function here -

http://www.it.uom.gr/teaching/linearalgebra/NumericalRecipiesInC/c6-4.pdf

[sapfire]

My approach is this: if the matrix dimensions are both even, then Chef wins with both of the rules, if they’re both odd - Yoda wins with both of the rules, otherwise - there’s a 1/2 probability.
Then I divide the number of favourable combinations (i.e. where Chef win at least p times) by the total number of combinations.

For subtasks 1 and 2 I get AC, why is the code wrong in subtask 3?

CodeChef: Practical coding for everyone

Where is my mistake?

[kush2327]

bhisma probably taking a few test and drawing them out: cases of odd * odd, odd * even and even*even matrices of small sizes could help in understanding the result of a game.
Problem then reduces to finding kCi/pow(2,K) where p<=i<=k which can be done using log as others have mentioned.

[prakhar_26]

Instead of using log, we can keep dividing by 10 and store the exponent separately.

here is my solution

Please upvote, thanks

[vijju123]

@gonecase- (To others, the question he asked is in comment of bansal1232’s answer, just telling so no one gets confused )

Ah! I see. Its a good question that why we are generalizing our observations. While I am still beginner in game theory type of questions, I will try my best to explain.

We are given that they play optimally. When both the players play optimally, then win and loss are solely decided by starting conditions, which in this case are dimensions of board.

This type of question usually require you to spot the recurring condition whichs are causing loss or win.

Yes, there are MANY possible moves for high matrix, and yes, for some questions you might have to go through all possible moves to find the optimal moves chosen by them. (Hence why we prefer performing it on smaller cases and extend it to larger ones).

While it is possible to symmetrically/mathematically or conceptually prove the wins in this Q, it can get really tough.

Eg- Lets take a case of N and M being odd, and diagonal rule set is to be followed (meaning they can only move diagonally)

Lets say we have a 5x5 grid, and chef starts at 1,1.

The ONLY possible move for Chef is to move from 1,1 to 2,2. Now, YODA wants to win, and after some trials you will find his optimal move is to push it from 2,2 to 3,3. Now poor chef can either go to 2,4 or 4,2 or 4,4. And its easily seen that no matter WHERE he moves, he is going to lose (as after his move, YODA could force the coin to another corner, getting the win.)

What determined who won or not? There were two factors here-

1. Chef HAD to move from 1,1 to 2,2. No other possible move.
2. The Size of board favoured YODA when he played optimally.

Now you may want to argue for a 7x7 board.

7X7 BOARD

Chef moves to 2,2. Now YODA would force him BACK to 1,3. Chef would have ONLY 1 POSSIBLE MOVE, i.e. from 1,3 to 2,4. YODA will again make him go to 1,5 , then chef could only go to 6,2 , and then YODA wins by making final move at 1,7.

NOTE- The same strategy could also be followed in 5x5 board. Actually, MULTIPLE winning strategy exist for a particular N and M, and what we found in case of 5x5 was something specific to it, (or perhaps extensible to higher cases, didn’t check…too many possible moves).

NOTE 2 - We can interchange rows and columns here. Meaning If chef moves to 2,2, yoda can follow exact same strategy and move to 3,1 (& etc.) and win, provided that side is also odd.

(Also, I am sorry if I interchanged rows or columns in my explanation, please refer to image for clarity )

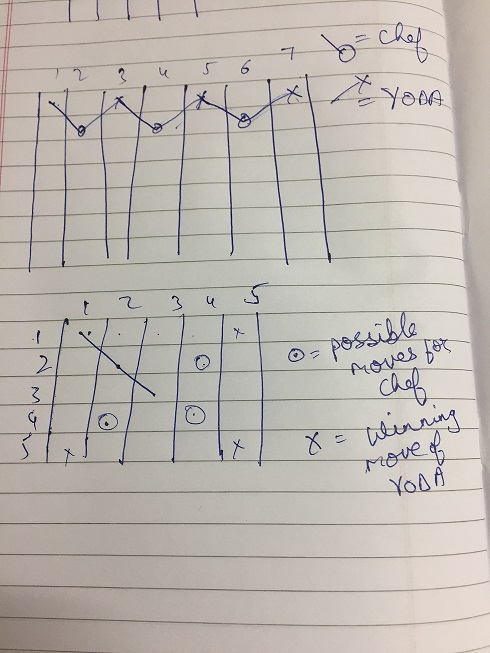
Here we found the true symmetry, and a concrete proof that at least one winning strategy for YODA EXISTS if both N and M are odd. YODA can play it every time N and M are odd. We can extend it to cases for 9x9,11x11 and so on. (Thus, for this case, extending of our base cases should work.)

And after concluding this, we might be interested in extending our base observations of other conditions to higher N and M. (Eg- When both even, when one even one odd etc.)

You CAN find other symmetries for other cases, but its tough. And problem setters expected us to conclude from observations.

Now, what if it fails? Had it failed, and we would had been unable to extend our base observations to higher ones, then we would be forced to either derive that when does winning strategy exist for CHEF/YODA (like we did above), OR there would be some hidden trick in Q for us to decipher.

I am sorry, I cant afford to go on deriving all possible cases at this moment ( Second Series of Exams from 31st…T_T pray for me ), but I hope I quenched your query. BTW, it was a good question you asked, I am sure it would help many other people with similar doubt.

(PS- If you look at the image for 7X7 carefully, you would realize that the same strategy YODA can play if either one of N and M are even (because effectively everything is happening in the 2X7 matrix.) Meaning he can play this and win if N odd and M even. This when DIAGONAL rules are to be followed. When diagonal rules are not followed, we can prove that chef would win. (The strategy he’d use is to go from 1,1 to 1,2 [1 cell down], forcing YODA to go from (2,2) and similarly win. (I thin you must have derived it in 2x2 and 2x3 type of matrices) )

[shbhm_53]

Just used some property of logarithms.

Here’s my code

[chan55555]

For the diagonal move rule (Rule 2), I got the proof of “why does Yoda win when either side of the matrix is odd”. But for the other rule, I didn’t find any solid proof of the winning conclusions. Are they just derived from observations or there is any proof?

[hemanth_1]

Nice! I thought of that, but was not so sure about the precision

[sdssudhu]

Since for the third case (the case in which your program failed) had n<=1000 you could have used DP itself for an AC.

Also I tried solving this using the normal approximation but I could not get it in the 4th case and went for log properties.

[likecs]

Short and effective.

[bhishma]

The link that you’ve attached is broken

[aditya211935]

Sorry! It’s fixed now.

[gonecase]

@bansal1232 , Could you please explain logic that you used to decide that if N, M are even/odd, Chef/Yoda will be the winner. I tried to draw a 4 x 4, 4 x 5 grid, etc, to understand why, but couldn’t figure out what the logic was because there are so many moves possible.

[vijju123]

Don’t start with 4x4 or 4x5!

Start with 1x1 and slowly proceed till 3x3. Try it once, and if its still unclear, I can help.

[gonecase]

@vijju123, I made decision trees for tables of size 1x1, 1x2, 2x3, and 3x3. I can see that Yoda wins every time M and N are odd if we are playing with rule set 1 and Chef wins every time either M or N is even. But I fail to understand why this can be generalized to higher dimensions/values of M and N. My question is, how can we be sure that just because it worked till M, N <= 3, it will work for M, N>3. And also, what I didnt understand was if there is some optimal strategy that is there. For example, if Chef makes such and such a move, Yoda must make a move that fulfills certain conditions??

[gonecase]

@vijju123, Thanks for taking your time out. I got a better idea of the solution.

[vijju123]

I am glad it helped. :).

The basic proof that we can extend our base solutions is existence of at least one winning strategy for CHEF/YODA (which they can repeat everytime the board dimensions are favourable) for some pattern in dimensions.