PROBLEM LINK
DIFFICULTY
easy
PREREQUISITES
graph theory, Dijkstra’s algorithm, transforming graph into similar graph
PROBLEM
You are given a undirected weighted graph consisting of n vertices, and m edges. Initially there is no edge between any pair of first K vertices. We add the edge between each pair of first K vertices of weight X (i.e. the first K vertices form a clique). Given a source vertex s, find out the shortest distance of each node from vertex s.
Finding the shortest distance in a weighted graph from a fixed source vertex is a classical problem. There is a famous greedy algorithm called Dijkstra’s algorithm which can solve this problem in \mathcal{O}((|V| + E|) log (|V|)) time.
If we directly apply the Dijkstra’s algorithm in our problem, the number of vertices, i.e. |V| = n, and the number of edges, i.e. |E| = m + \binom{K}{2} (due to the clique). Hence, the time complexity of this algorithm will be \mathcal{O}((m + K^2) \, log (n)), which is enough to solve the first subtask, but won’t be sufficient to solve the final subtask.
Solution by constructing another graph
One of the ways of dealing with such situations is to think whether it is possible to convert the given graph into another graph that doesn’t have \mathcal{O}(K^2) edges of the clique added in it, and yet it preserves the pairwise distances of the vertices of the original graph.
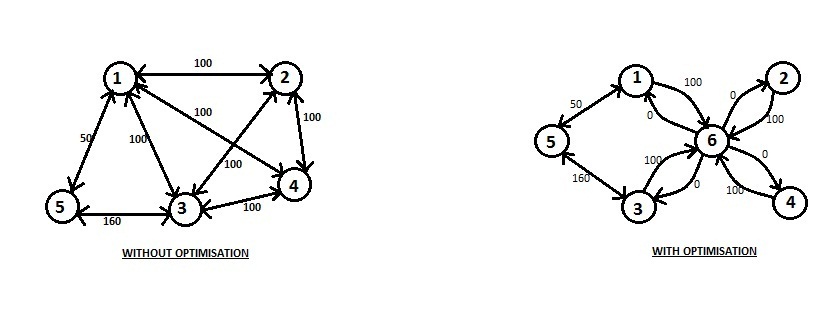
We can do this in the following way. Let us create a fake vertex. This fake vertex will be connected to the each of the first K vertices. The weight of each edge will be \frac{X}{2}. So now, instead of the first K vertices being connected in the form of clique are connected to the fake vertex in the form of a star topology where the central node of star is the fake vertex.
// Add an image.
Thus we have K edges in the modified graph instead of K^2 edges of the original graph. The remaining edges in the modified graph will remain same. Notice that the distances in the modified graph are precisely the same as that of in the old graph. Here the edge connecting vertices u and v (where u, v \leq K) with weight X directly has been replaced with the u being connected with fake vertex with distance \frac{X}{2}, and from the fake vertex with v with distance \frac{X}{2}.
Apply Dijkstra’s algorithm on this modified graph will yield a time complexity of \mathcal{O}((m + K) log (n)) which will give you full score.
A small detail which can be useful here. As the number \frac{X}{2} will not be an integer when X is odd. So, instead of dealing with non-integers (reals) in the Dijkstra’s algorithm, you can multiply all the distances by 2 to make all the distances even. Finally you divide the final distances by 2 to get the actual answer. In this way, you will never have to deal with real numbers.
Solution by applying the usual Dijkstra with a little twist
You can apply the usual Dijkstra’s algorithm. Let d[i] denote the distance of vertex i from source vertex s. When you are first time processing one of the vertices belonging to the clique, say vertex u, you consider the distances of all other vertices in the clique to be d[u] + X. Afterwards, whenever you encounter a vertex in clique, you need not to go over the clique edges to relax the distances of clique vertices. This algorithm will make sure that your time complexity is \mathcal{O}((m + K) log (n)), as instead of processing all the K^2 edges of clique, you are processing only K of them.
A solution by trusting your intuition and implement direct Dijkstra with a bit modification.
One might intuitively think that the number of relaxations in the Dijkstra’s algorithm might be m + K instead of m + K^2. Proof of this intuition lies in the understanding of previous algorithm.
You can directly implement this algorithm. You maintain a set (balanced binary search tree) of the clique vertices sorted by their distances in the increasing order. You can find the set of vertices to relax by making a search in the set. This way, you will only be relaxing the vertices only among the necessary vertices in the clique. See the editorialist’s solution for a sample implementation of this approach.