PROBLEM LINK:
Author: Mikaeel
Tester: Hanlin Ren
Editorialist: Hanlin Ren
DIFFICULTY:
Medium-Hard
PREREQUISITES:
Trees, Depth First Search, Segment Tree / Fenwick Tree
PROBLEM:
There is a rooted tree of N vertices, and some vertices contain bacteria. In every second:
- Every bacterium in a non-leaf vertex v splits into d copies, where d is the number of children of v.
- Then each copy goes to a distinct children.
- Bacteria at leaves doesn’t move, split or disappear.
You need to process q seconds. In the i-th second you’re required to either put k_i new bacteria to vertex v_i, or output the number of bacteria currently at the vertex v_i.
QUICK EXPLANATION:
- We process the seconds (i.e. queries) in ascending order of i-dep(v_i), where i is the time of that query, dep(v_i) is the depth of the vertex that query works on.
- We maintain two copies T_{\sf leaf},T_{\sf nonleaf} of the input tree, one for leaf queries and one for non-leaf queries.
- For each query “+ v_i k_i”, add value k_i to every node in the subtree of v_i (in both trees).
- For each query “? v_i”, if v_i is a leaf, output the value of v_i in T_{\sf leaf}, otherwise output the value of v_i in T_{\sf nonleaf}.
- Recall that we iterate through the queries by nondecreasing order of i-dep(v_i). Whenever this number changes (i.e. increases), clear all values in T_{\sf nonleaf}.
EXPLANATION:
Notation: let’s denote the operation in the i-th second be either “+ v_i k_i”, or “? v_i”. That is, v_i is always the vertex operated in the i-th second, and k_i is the number of bacteria added to v_i if in the i-th second we put bacteria in v_i.
We start with an observation. Consider a bacterium which is at vertex v in the i-th second. As it (technically, one of its copies) goes down the tree, if it hasn’t reached a leaf node, then the difference between its depth and the time doesn’t change. In other words, if it’s at vertex u in the j-th second (and u is not a leaf), then i-dep(v)=j-dep(u). The proof is simple: each second its depth increases by 1. Given this observation, the following definition may be useful. For the query in the i-th second, let’s denote E[i]=i-dep(v_i).
Let’s consider the i-th query and suppose it is of the form “? v_i”. There are two cases.
Case 1: v_i is not a leaf. Consider all queries of the form “+ v_j k_j”. This query contributes to the i-th query, if and only if the following two conditions hold:
- E[j]=E[i], i.e. j-dep(v_j)=i-dep(v_i);
- v_j is an ancestor of v_i.
(We may want a third condition that j<i as well, but that’s already implied by the above two conditions.)
Therefore, we group these q seconds by their E[\cdot] values. For each group (with the same E[\cdot] value), the problem becomes:
- For each query of the form “+ v_j k_j”, simply add k_j bacteria to the node v_j;
- For each query of the form “? v_j”, output the total number of bacteria in the ancestors of v_j.
(Note that in this case, queries in different groups does not influence each other.)
Or equivalently:
- For each query of the form “+ v_j k_j”, adds k_j bacteria to every node in the subtree of v_j;
- For each query of the form “? v_j”, output the number of bacteria in the vertex v_j.
This is a very standard data structure problem on trees, and by using segment trees or Fenwick trees to maintain the DFS order, we can solve the problem in O((n+q)\log n) time.
If you don't know how, please read this.
First, we need to compute the DFS order of a tree. The DFS order is the order of nodes that we encounter during a Depth-first search, and it can be computed by the following pseudocode:
DFS(x)
push vertex x to the DFS order
for (v in children of x)
DFS(v)
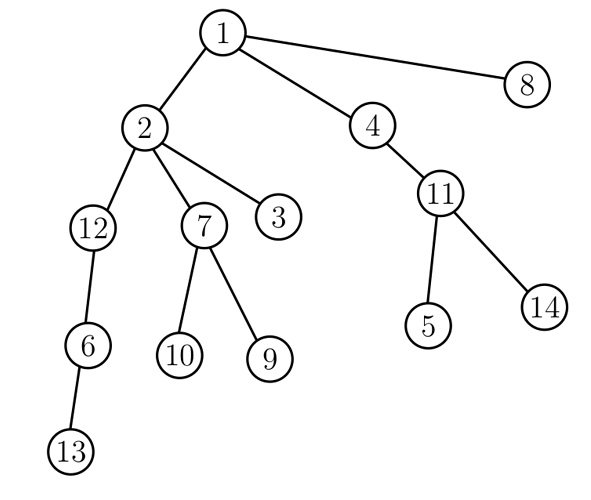
For example, a possible DFS order of the tree below is (1,2,12,6,13,7,10,9,3,4,11,5,14,8).
A good property of DFS order we will use is that, every subtree corresponds to an interval of the DFS order. For example, the subtree of vertex 2 corresponds to the interval (1,{\bf\color{red} 2,12,6,13,7,10,9,3},4,11,5,14,8), and the subtree of vertex 11 corresponds to the interval (1,2,12,6,13,7,10,9,3,4,{\bf\color{red}11,5,14},8).
Let [l[i],r[i]] be the interval corresponding to the subtree of the i-th vertex. In the above example l[2]=2, r[2]=9, l[11]=11, r[11]=13. To compute l[i],r[i], we maintain the number of visited vertices in our DFS algorithm. Whenever we enter x, l[x] is the number of visited vertices; whenever we leave x (so we’ve processed the subtree of x), r[x] is (also) the number of visited vertices.
global variable num_of_visited_vertices
DFS(x)
push vertex x to the DFS order
num_of_visited_vertices++
l[x] = num_of_visited_vertices
for (v in children of x)
DFS(v)
r[x] = num_of_visited_vertices
Now we maintain an array A[1\sim n] and process the queries. Let DFS[i] be the i-th node in the DFS order, initially A[i] is the number of initial bacteria in vertex DFS[i]. When we add k_j bacteria to the subtree of v_j, we add k_j to the every element in the segment A[l[v_j],r[v_j]]. When we query about the number of bacteria in vertex v_j, we output A[l[v_j]]. (Note: by the above algorithm we can see that v_j is the l[v_j]-th vertex in the DFS order. Therefore the number of bacteria on v_j is stored in A[l[v_j]].)
The problem becomes the following (really) classical problem: given an array, support range addition and point query. We can solve this problem by segment trees or Fenwick trees.
Case 2: v_i is a leaf. The situation is very similar. A modification + v_j k_j contributes to the query ? v_i, if and only if the following two conditions hold:
- E[j]\le E[i], i.e. j-dep(v_j)\le i-dep(v_i);
- v_j is an ancestor of v_i.
(Note that j<i still follows from the above conditions.)
We sort the q seconds by ascending order of E[\cdot], then iterate through them. If the current second is a modification + v_j k_j, we add k_j bacteria to every vertex in the subtree of v_j. If it’s a query ? v_j, we output the number of bacteria in v_j. We can still use the aforementioned DFS-order based solution. The time complexity is still O((n+q)\log n).
Implementation Details. We can actually solve Case 1 and Case 2 simultaneously.
- We maintain two segment trees (or Fenwick trees if you like), one for Case 1 and one for Case 2.
- We still visit all operations by ascending order of E[\cdot]. Each time we meet a modification (query resp), we perform a subtree addition (point evaluation resp).
- When the E value of the current operation changes (i.e. increases), it means that we reached a new group of operation (in Case 1). Therefore we clear the first segment tree, and proceed as usual.
- To clean a segment tree, we can’t iterate through all its nodes, since otherwise the time complexity degenerates to O(nq). Instead, we undo the operations that we did in the last group.
- The time complexity is still O((n+q)\log n).
ALTERNATE EXPLANATION:
Please feel free to share your approaches ![]()
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
#define put(x) cout<<#x<<" = "<<x<<endl;
using namespace std;
const int maxn=2e6+10,maxq=4e6+10;
const char addQuery='+',askQuery='?';
struct Query{
int id,time,v,k;
long long answer;
char type;
Query(){}
Query(int _id,char _type,int _time,int _v,int _k=0,long long _answer=0){
id=_id;
type=_type;
time=_time;
v=_v;
k=_k;
answer=_answer;
}
};
int n,q,H[maxn];
int qsize=0,startingTime[maxn],finishingTime[maxn],curTime=0;
long long A[maxn];
bool isLeaf[maxn];
vector<int> G[maxn];
Query Q[maxq];
int Qper[maxq];
void dfs(int a,int par=-1){
startingTime[a]=curTime++;
for(int b:G[a]){
if(b!=par){
H[b]=H[a]+1;
dfs(b,a);
}
}
if(int(G[a].size())-(par!=-1)==0){
isLeaf[a]=1;
}
finishingTime[a]=curTime;
}
struct FenwickTree{
long long s[maxn];
bool mark[maxn];
int history[maxn],historySize=0;
void add(int x,long long value){
x+=5;
if(!mark[x]){
mark[x]=1;
history[historySize++]=x;
}
for(int i=x;i<maxn;i+=i&-i){
s[i]+=value;
}
}
// [L,R)
void add(int L,int R,long long value){
add(L,+value);
add(R,-value);
}
long long ask(int x){
x+=5;
long long ans=0;
for(int i=x;i>0;i-=i&-i){
ans+=s[i];
}
return ans;
}
void clear(){
for(int i=0;i<historySize;i++){
int a=history[i];
mark[a]=0;
for(int j=a;j<maxn;j+=j&-j){
s[j]=0;
}
}
historySize=0;
}
}fenwick[2];
int32_t main(){
scanf("%d%d",&n,&q);
for(int i=0;i<n-1;i++){
int a,b;
scanf("%d%d",&a,&b);
a--,b--;
G[a].push_back(b);
G[b].push_back(a);
}
dfs(0);
for(int i=0;i<n;i++){
scanf("%d",A+i);
// this query doesn't need to have a valid id
Q[qsize++]=Query(maxq,addQuery,-H[i],i,A[i]);
}
for(int i=1;i<=q;i++){
Q[qsize].id=i;
scanf(" %c",&Q[qsize].type);
if(Q[qsize].type==askQuery){
scanf("%d",&Q[qsize].v);
Q[qsize].v--;
Q[qsize].time=i-H[Q[qsize].v];
}else if(Q[qsize].type==addQuery){
scanf("%d%d",&Q[qsize].v,&Q[qsize].k);
Q[qsize].v--;
Q[qsize].time=i-H[Q[qsize].v];
}else{
assert(0);
}
qsize++;
}
for(int i=0;i<qsize;i++){
Qper[i]=i;
}
sort(Qper,Qper+qsize,[](int a,int b){
if(Q[a].time!=Q[b].time){
return Q[a].time<Q[b].time;
}
// For queries with the same time, addQuery has more priority
return Q[a].type=='+' && Q[b].type=='?';
});
for(int i=0;i<qsize;i++){
if(i>0 && Q[Qper[i-1]].time!=Q[Qper[i]].time){
fenwick[1].clear();
}
if(Q[Qper[i]].type==addQuery){
fenwick[0].add(startingTime[Q[Qper[i]].v],finishingTime[Q[Qper[i]].v],Q[Qper[i]].k);
fenwick[1].add(startingTime[Q[Qper[i]].v],finishingTime[Q[Qper[i]].v],Q[Qper[i]].k);
}
if(Q[Qper[i]].type==askQuery){
int fenwickId=1;
if(isLeaf[Q[Qper[i]].v]){
fenwickId=0;
}
Q[Qper[i]].answer=fenwick[fenwickId].ask(startingTime[Q[Qper[i]].v]);
}
}
for(int i=0;i<qsize;i++){
if(Q[i].type==askQuery){
printf("%lld\n",Q[i].answer);
}
}
}
Tester's Solution
#include <bits/stdc++.h>
using namespace std;
#define sz 500200
#define next nnext
#define sum ssum
typedef long long ll;
template <class Q> void gi(Q &x) {char ch = getchar(); x = 0; while (ch < '0' || ch > '9') ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - 48, ch = getchar();}
template <class Q> void pi(Q x) {if (x > 9) pi(x / 10); putchar(x % 10 + 48);}
char gc() {char ch = getchar(); while (ch != '+' && ch != '?') ch = getchar(); return ch;}
int n, q;
int node[sz], next[sz << 1], to[sz << 1], e;
void ins(int x, int y) {e++; next[e] = node[x]; node[x] = e; to[e] = y;}
int dep[sz], par[sz];
bool isleaf[sz];
int seq[sz], I, st[sz], ed[sz];
void dfs(int x, int p) {
seq[st[x] = ++I] = x;
for (int j = node[x]; j; j = next[j])
if (to[j] != p) {
par[to[j]] = x; dep[to[j]] = dep[x] + 1; isleaf[x] = 0;
dfs(to[j], x);
}
ed[x] = I;
}
void init() {
int i, u, v, k;
gi(n); gi(q);
for (i = 1; i < n; i++) {
gi(u); gi(v);
ins(u, v); ins(v, u);
}
for (i = 1; i <= n; i++) isleaf[i] = 1;
dfs(1, -1);
}
char qc[sz << 1];
int qv[sz << 1], qk[sz << 1];
int qtm[sz << 1], next2[sz << 1], to2[sz << 1], e2;
void ins2(int x, int y) {e2++; next2[e2] = qtm[x]; qtm[x] = e2; to2[e2] = y;}
ll a1[sz], a2[sz], ans[sz];
void add(ll *a, int x, int y) {for (; x <= n; x += x & -x) a[x] += y;}
ll sum(ll *a, int x) {ll s = 0; for (; x; x -= x & -x) s += a[x]; return s;}
#define ADD(a, l, r, y) add(a, l, y), add(a, r + 1, -y)
void query() {
int i, j, k;
for (i = 1; i <= n; i++) {
qc[i] = '+'; qv[i] = i; gi(qk[i]);
ins2(n - dep[i], i);
}
for (i = 1; i <= q; i++) {
qc[j = i + n] = gc();
if (qc[j] == '+') gi(qv[j]), gi(qk[j]);
else gi(qv[j]);
ins2(n + i - dep[qv[j]], j);
}
for (i = 1; i <= n + q; i++) {
for (j = qtm[i]; j; j = next2[j]) {
k = to2[j];
if (qc[k] == '+')
ADD(a1, st[qv[k]], ed[qv[k]], qk[k]),
ADD(a2, st[qv[k]], ed[qv[k]], qk[k]);
}
for (j = qtm[i]; j; j = next2[j]) {
k = to2[j];
if (qc[k] == '?') {
if (isleaf[qv[k]]) ans[k - n] = sum(a2, st[qv[k]]);
else ans[k - n] = sum(a1, st[qv[k]]);
}
}
for (j = qtm[i]; j; j = next2[j]) {
k = to2[j];
if (qc[k] == '+') ADD(a1, st[qv[k]], ed[qv[k]], -qk[k]);
}
}
for (i = 1; i <= q; i++)
if (qc[i + n] == '?') pi(ans[i]), putchar('\n');
}
int main() {init(); query(); return 0;}