what is prime(0)?
provide the link of full code with your template
Thanks for the great explanation. Will Codechef provide the data used to test possible solutions? It would be useful knowing for what cases my code fails. Thanks again. Cheers.
can you explain this test case:
input: 30 90
output: 3
prime factors are 2 3 5
then how will you divide into different columns as their lcm is 30
please given me possible column size
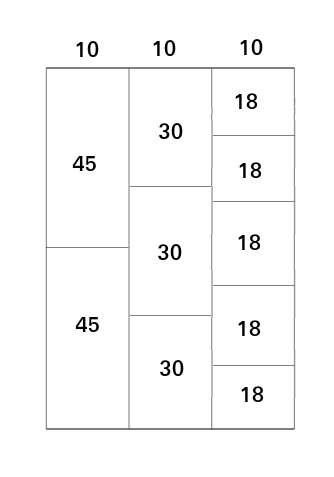
Here’s an entirely random test case for which your code fails.
Input
1
2 1885387
Expected Output
2
Your Output
1
Explanation:
The Screen of width 2 can be divided into two columns, with the heights of windows being 269341 and 7.
thanks
Are there any corner test cases for this question? My code is giving wrong answer for the final test case
Can you elaborate on your thesis using the following test case?
Input
1
210 1050
Also, show how you can attain the maximum number of Columns just by using Prime Factors.
Is this the counter example of what is I just above (according to you) ?
If yes, then please elaborate!
Thanks, updated!
Can anyone tell me why my code is failing.I have checked some test cases also
here’s my submission
https://www.codechef.com/viewsolution/56021154
I have a doubt regarding a corner case, which is, N=4, M=20
Editorialist solution’s output is 2.
But output should be 1.Because the answer takes two prime factors into consideration, which are: 2 and 5. (Prime factorization of 20 : 2 * 2 * 5)
But, there y coordinate will match at y=10, because LCM(2,5)=10.
So, this is a contradiction, right?
Can someone clear this doubt?
Please clear this doubt, @pranavreddyp16 @lavish315 @tejas10p @ajit123q
According to the convention taken in the editorial the LCM of sizes of windows should be considered so as to see if they meet at a point (si and sj), not the count of windows. Furthermore, si and sj should be a multiple of m (if they have remainder left then last window will not be of equal size). Therefore, there LCM is going to m in any case, you can’t have more than that . LCM(si,sj) < m is obviously not gonna help us as then the windows will meet at a horizontal level below y = m. Therefore the only option left is LCM(si,sj) = m.
LCM(si,sj) = m
And this is bascially going to lead us to the same conclusion. Consider the following proof,
LCM(si,sj) = m
⇒ LCM(m/ci,m/cj) = m
⇒The last implication basically means that even after removing factors common to ci from m and then factors common to cj from m we get the LCM still as m. This means that ci and cj must have no common factors in it (except 1 obviously) .
=>GCD(ci,cj) = 1
Hence, both the logic are equivalent and lead to the same conclusion.
*do let me know if you find anything wrong *
Thanks
According to the convention taken in the editorial the LCM of sizes of windows should be considered so as to see if they meet at a point (si and sj), not the count of windows. Furthermore, si and sj should be a multiple of m (if they have remainder left then last window will not be of equal size). Therefore, there LCM is going to m in any case, you can’t have more than that . LCM(si,sj) < m is obviously not gonna help us as then the windows will meet at a horizontal level below y = m. Therefore the only option left is LCM(si,sj) = m.
LCM(si,sj) = m
And this is bascially going to lead us to the same conclusion. Consider the following proof,
LCM(si,sj) = m
⇒ LCM(m/ci,m/cj) = m
⇒The last implication basically means that even after removing factors common to ci from m and then factors common to cj from m we get the LCM still as m. This means that ci and cj must have no common factors in it (except 1 obviously) .
⇒GCD(ci,cj) = 1
Hence, both the logic are equivalent and lead to the same conclusion.
*do let me know if you find anything wrong *
Thanks
Exactly, this is what I am having a doubt.
I guess you wanted to say “si” instead of “ci”.
Adding to your point, take the case when N=4, M=20
Ouput should be 1, but the solutions mentioned in the editorial is 2, which is wrong according to problem statement.
Please clear this doubt, @pranavreddyp16 @lavish315 @tejas10p @ajit123q
I guess you are again confusing ci with si. Considering prime factors of 20 i.e 2 and 5 will give ci values. So, let ci = 2 and cj = 5 (number of windows in a column) then si = 10 and sj = 4 (sizes of every window in a column). Using these sizes we can see that they will never meet at a horizontal level. (SEE THE IMAGE ATTACHED).
You haven’t understood the question properly. Try reading the question again.
 Welcome!
Welcome!
