How to do this using permutation and combination

general
, , ,
16

It won’t work for special cases where N \leq 2 because we have N-3 in the exponent. But the answer is (K-1)K when N =2 and K-1 for N = 1 because we can’t have a 0 in last digit.

17

Can you please tell what inputs you’re talking about?

18

I am pretty sure somethings wrong, please run this code to see your method and dp:

19

What was the input?

20

It’s giving WA for almost every input. Did you check ?

21

You’re right. What went wrong? And why do the samples work?

1 Like
22

It works for n=3 only.
I cwont be able to sleep if I dont solve this problem :zipper_mouth_face:

23

What complexity are you looking for?

1 Like
24

Me too. @galencolin, please check my formula and let me know what’s wrong. I don’t know where I went wrong.

1 Like
25

Your idea is wrong. First, you have to account for the n - 2 possible positions for the pair of zeros. And also, you aren’t counting strings that have more than one consecutive pair of zeros.

That means there’s no quick fix you can do to correct it, as it’s more complex than your formula would be

2 Likes
26

If we have atleast one consecutive pair of zero, then all other n-3 position can have any digit including zero.

Wont this include that case ?

1 Like
27

Thanks. Is a solution with combinatorics even possible?

28

(As an example,) take n = 4. You’ll count both strings of the form x00 and 00y, right? But if x = y = 0, you’ll count the string 000 twice. This effect is magnified as n grows.

2 Likes
29

okay, I think it might overcount…

30

Not sure, thinking about it myself, but I’m also weak in combo

2 Likes
31

Even if there’s a combo solution, it’s very likely that there isn’t one with asymptotics better than O(n), because you can represent the answer in the form \sum\limits_{i = 0}^{n}{c_i \cdot (k - 1)^{n - i}}, where c_i is the count of n-digit numbers with exactly i zeros. In all my life I’ve never seen a way to optimize a formula like this.

2 Likes
32

@galencolin By combinatorics, the formula comes out to be 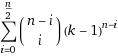image
Now using wolfram alpha we get-Link or Link:slight_smile:

2 Likes
33

Can you explain ?

34

Yes

35

Even after convincing myself of that identity’s correctness in the past, I still don’t understand it lol