Simplest approach I think just iterate over n*n matrix and query for sub matrices of 1 size… Amd check for answer to thr query…
Further you can optimise the solution bh keeping total counts of 1’s in whole matrix and keep track of how many times 1 occur and breaks the loop when count become zero.
I didn’t get Ac but it was giving WA
Here is my approach. (44/100)
first query for whole matrix get total 1s
now find rows and colms in following way.
query for row 2 to n and colms 1 to n subtract from tot got row1( add it to sum )
query for row 3 to n and colms 1 to n row2=total-query-sum (add row 2 to sum)
repet untill n/2 and for remaning n/2 start from reverse (n to n/2)
same for colms.
try to fill matrix as much as you can
if row[i]=0 fill whole row with 0 or row[i]=remaining in row[i] fill whole with 1s
Last step.
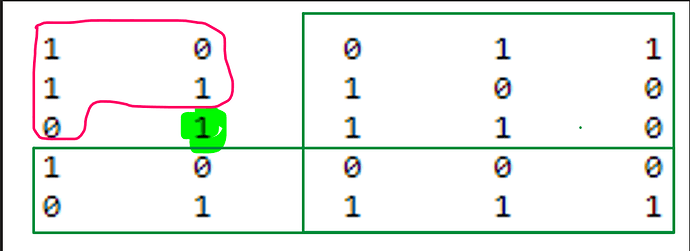
start from left corner in following way
you can get sum of all rows under element by summing all rows found earlier same for colms right to element
and can also get sum of processed part(as we started from left corner) by adding all ones from 1 to i and 1 to j
then query for common green box (i+1 to n and j+1 to n) as shown in figure and ans
is a[i][j]=tot-sum(rows,i+1,n)-sum(cols,j+1,n)-ones in matrix (1 to i)row and (1 to j) cols) +query for common part.
I tried binary search at every row.
it can be further improved by filling matrix such that common box is as large as possible
i.e.
divide matrix in 4 parts from mid and fill one by one
first 1 to n/2 and 1 to n/2
second 1 to n/2 and n to n/2 (or n/2 to n)
third n/2 to n and 1 to n/2
I got about 28 points. Here are the main ideas:
- Consider rows and columns in increasing order, at each step try to compute the cell value.
- For cases when row <= n/2 and col <= n/2, query (row,col,n,n), (row+1,col,n,n),(row,col+1,n,n) and (row+1,col+1,n,n). Combination of these 4 values easily gets the cell value at (row,col). Once the query is made for some rectangle, keep it in memory so that we don’t send query for it again.
- For other quadrants (row>n/2, col<n/2 etc) choose the rectangles appropriately, to make them as large as possible.
- Note that the highest cost will generally occur when p = 2. Nice thing for p=2 is that there are very few ones. To take advantage of this, at the beginning of each row compute the row sum (by querying (row, 1, n/2, n) and (row+1,1,n/2,n) and when they are equal, skip first n/2 columns of this row. This will happen about 55% of the time. If not, solve each quadrant the same way. Do similar trick for the columns n/2 + 1, …, n.
- Another optimization (although didn’t have time to submit this) can be to split initial matrix into blocks of size b and do something like: for cell (r,c), query (r,c,n,n), (r,c+b,n,n), (r+b,c,n,n) and (r+b,c+b,n,n). This gives us sum in square (r,c,r+b,c+b). If it’s 0, we can skip all these cells in future. The value of b can be chosen depending on p. b=5 works well for p=2 and b=2 works better for p>=5.
Hope this helps 
Using a 2D dichotomy over the entropy and using some deduction rules I got the best score in the 2nd division. The main idea is to construct a recursive function f that compute a submatrix of A by dividing it in 4 submatrices and calling f over this 4 new submatrices. Before calling f on a rectangle (r1, c1, r2, c2) you need to compute the number of ones in all rectangles (1, 1, i, c1), (1, 1, i, c2), (1, 1, r1, j) and (1, 1, r2, j) for r1 \leqslant i \leqslant r2 and c1 \leqslant j \leqslant c2. CodeChef/COVDSMPL.cpp at master · Nanored4498/CodeChef · GitHub
I never thought that P can be useful 
it is nice idea to skip the n/2 part.
I finally got 78 points in div1.
My stupid method is to preprocess the sum of each column and then ask each row in half. If this sum is 0 or the sum is the area, then you can directly fill in the number.
Note that each time you ask about a rectangle, choose a large rectangle with one of the four corners as its vertex to ask about it, and should reasonably use the previous inquiry results to infer.
In this way, about 60 points can be reached.
Brother, you are my idol 

Wait What? Binary Search? can you please elaborate or at least post your solution friend.
Okay, ~70 pt (div. 1) solution here:
In basic terms, I’m simply recursively traversing the entire matrix. If the current submatrix has only 0’s or only 1’s, I exit the current iteration. Else I split into two halves and go deeper.
However without optimizations this gets < 1 pt.
Several possible ways to make this cost less:
-
As @kk2_agnihotri correctly pointed out, bigger matrices cost less, so when I receive an order to query a certain submatrix, I try several ways to find the sum in it through other sums. For example, by doing a prefix-sum-like (or suffix-sum-like) technique. I also try calculating the entire horizontal strip, extended down (or up) and then simply subtract the extra elements. Same with vertical strips. I calculate the expected cost of each of these options and simply choose the cheapest.
-
It is possible to keep already calculated queries in a map so as not to do unnecessary work. I set the expected value for such a query (that has already been asked before) as 0, however in earlier versions I used numbers all the way down to -200 (well, I was kinda experimenting with constants as well).
-
Expanding on the idea in (1), we can make the following improvement. Say we have a submatrix whose sum we are about to ask the judge. We notice that if the horizontal strip right above it is already calculated, we can add it to the submatrix and simply subtract the sum from the final answer. The cost of the query will thus only decrease. Same with the horizontal strip below and the two vertical strips to either side.
-
Another, but as far as I can remember, insignificant improvement. If the submatrix about to be sent to the judge can be split into two submatrices with already calculated sums, we can return the sum of the two sums and avoid asking anything altogether.
In the earlier submissions I had been also trying to calibrate various constants (which worked btw!), but in the highest-scored submission there is absolutely no calibration (actually that only worsens the performance, lol…)
I’ve looked at several other top-scoring submissions. Their authors use Fenwick tree to calculate sums. I just did brute-force, I didn’t really need any fast algorithms, and most of my submissions actually had a runtime of 0.00 (before the part when I included point 4).
Hope I explained this more or less clear, and yes, the thought process was not linear, I came to those ideas in a week in total, so it wasn’t like I suddenly thought of something and got 70 points. I was rather close to the upper limit of submissions btw 
Rank1 of div1 is 28w 

Oh sorry it happened in last two hours
I didn’t observed latest.
I also have a doubt, has anyone tried probabilistic algorithms, such as Bayesian statistics?
I did, and it would work for n <= 10 easily, possibly for slightly larger n too, but for n=60 even if you’re 99% sure about some values, once in 3600 times it will almost always get something wrong. I didn’t explore it very deeply, maybe I could’ve done something better.
What I did was, I precomputed (using simulations) the following:
prob[rowSum][colSum][0/1] -> probability that sum of all cells in row is rowSum, similarly for columns and frequency of this event with grid[row][col]=0/1. To account for conditional probabilities (as we slowly gain more knowledge about the cells), I adjust this to be:
prob[cellCount][sum][0/1] to define the probability of 0/1 in a cell if there are cellCount unknown rows in it’s row and column in total and their sum is ‘sum’. At best, it was getting about 10 cells wrong in 60x60 matrix on average.
Another thing possible is to see the probability of 0 or 1 in a cell and only if it’s >99% or something declare it as such, otherwise do costly queries to find exact value. I tried this too, but even 99% was not too reliable. My guess is that n=60 was chosen partially to disallow this kind of approach.
not me

I had the 2nd or 3rd highest score in division 1.
Here’s what I did.
First calculate total number of 1s in each row and each column, now ignore the rows and columns with all 0s.
Then I’ll binary search in each row to find the exact position of the 1s. Also, I’ll keep subtracting the found elements from the corresponding columns.
I also maintain the prefix_sum of the part of the grid I’ve already found. It helps me get elements of next row by querying larger rectangles and subtracting the found prefix_sum.
This solution was around 80 points.
To improve further, I divided the grid into 6X1 blocks. 600 blocks in total.
Used the same binary search approach to get the values in each block.
On an average there would be around 0 to 3 positives in each block and a lot of blocks would be empty.
Now once this precomputation is done, binary search again to exact cells while being aware of the blocks and rows and columns.
Apart from this I also used a lot of micro-optimizations, some of them are:-
If the upper half has more elements than lower half then invert the grid upside down.
Store all queries in a map to avoid redundancy.
While querying if the row or column just outside your query rectangle is empty, include it in your query as it won’t change the answer
If the possible candidates in a row are less than half of the total positives in the row, then the search space is too congested, now it is better to Binary search to find the 0s instead of 1s.
And some other micro optimizations.
I had one more significant optimization but I couldn’t implement it before the time ran out
Brother, could you post a code?  I’d better do only 1/3 of the correct rate. I want to know more about it
I’d better do only 1/3 of the correct rate. I want to know more about it
You are a master of optimization.