its contests like these which makes me wonder whether cp is something for a retard like me
maybe i should start selling mangoes and watermelons in the streets of calcutta
3 Likes
Cool problems, How did you guys do Stack of Rectangles? My idea was to express the area of the stack in terms of the y coordinates and then use lagrangian multiplier over them but I wonder if there’s a simpler way to do it.
Hey everyone, we hope you enjoyed the contest. Please provide us with your valuable feedback.
You can solve it using similar triangles. For detailed explanation, we will release the editorials in some time.
1 Like
I think problems were hard enough for this contest to be rated for Div1 too.
3 Likes
pls see this and explain why this happen
1 Like
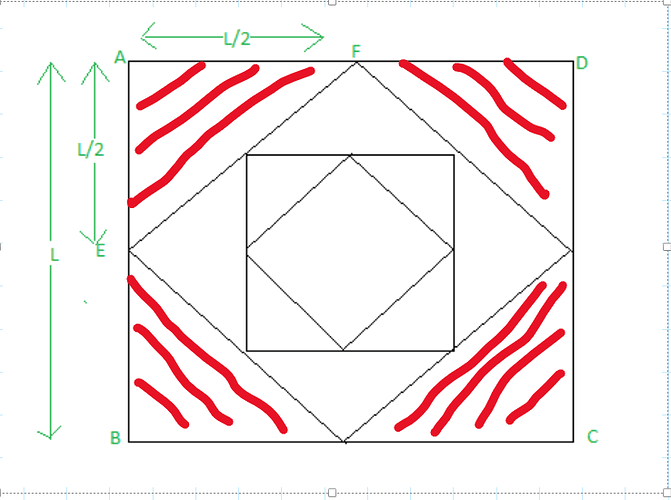
Can someone explain the infinite polygon solution?
Rotated sorted array is only possible array to fix. rest is impossible to do.
let theta=((n-2)*180)/n;
theta=theta/2;
ans= 1/(1-(sin(theta in radians))^2).
code.
double ang=(n-2)*90;
ang/=n;
ang*=M_PI;
ang/=180.0;
long double x=sin(ang);
x*=x;
x=1.0-x;
x=1.0/x;
cout<<fixed<<setprecision(16)<<x<<endl;
why is expectation not taken as E(X) = Sigma xi*P(X=xi) ? X is random variable representing number polynomials the point is inside. And P is area of sub polynomials.
Also i still don’t understand that logic. Something i am missing but i don’t know what.
Do you have proof for this one?
1 Like
If the array can be sorted by any number of cyclic rotations, answer is yes, else no. For detailed explanation, we are going to release the editorial.
Not exactly but this may suffice
Area of polygon =A = (L^2 n)/[4 tan (180/n)] (Googled). L is length n is number of sides
. Ratio of the area of inner polygon to outer polygon depends upon. only L(Visible).
Also this l equals
sin(theta/2)= S/L (new polygon/ original polygon).
theta is equal to angle of polygon.
Now by some math we easily get that the expectation value is
1/ (1-(ratio in change in area)) . sum of decreasing GP.
which sums up the original formula.
1 Like
It’s a simple geometric progression. We can calculate the ratio of sides using trigonometry if we suppose the initial length of side is 1. Instead of raising to the power of n (in the formula), we can exclude that part because a fraction raised to some enormous number is close enough to 0 for it to be discarded. (I’ve calculated it raised to the power of 1e12 using binary exponentation, but that part was not necessary). The rest is just implementation.
EDIT: I was replying to dhruv788
Here’s my code which does all the necessary steps and doesn’t just take the formula (but essentially the same thing, just a bit easier to grasp, it took a good amount of guessing the exponent tho):
#include <bits/stdc++.h>
using namespace std;
long double binpow(long double n, long long k) {
long double res = 1;
while (k) {
if (k & 1) res *= n;
n *= n;
k >>= 1;
}
return res;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
int t; cin >> t;
while (t--) {
int n; cin >> n;
long double res = 1;
long double x = (n - 2) * 180.0 / n;
x = x / 360.0 * M_PI;
x = sin(x);
long double cur = x * x; // ratio of areas
cout << setprecision(13) << fixed << (1.0 - binpow(cur, 1000000000000LL)) / (1.0 - cur) << '\n'; // geometric progression
}
return 0;
}
2 Likes
You only need to know the definition of expectation to solve this problem.
Let X be the random variable corresponding to the number of players so
\mathbb{E}[X]=\sum_{i=1}^{\infty} i \times \mathbb{P}(X=i)
Few trivial results,
Area of N sided polygon of side length L_0 is given by
\displaystyle\ A_{L_0}=\frac{NL_0^2}{4 \tan(\frac{\pi}{N})}
Side of the polygon made by joining the midpoints of the sides
\displaystyle\ L_1=L_0 \cos(\frac{\pi}{N} ) \\
-\\
L_i=L_0 \cos^i(\frac{\pi}{N})
So all we need to do is find \mathbb{P}(X=i) for all i.
Let’s see what \mathbb{P}(X=1) is.
\displaystyle\ \mathbb{P}(X=1)=\frac{A_{shaded}}{A_{L_0}} \\
\mathbb{P}(X=1)=1-\frac{A_{L_1}}{A_{L_0} }= 1-\frac{L_1^2}{L_0^2}=1- \cos^2{\frac{\pi}{N}}=\sin^2{
\frac{\pi}{N}}
Similarly, if you work out the math then
\mathbb{P}(X=i)=\frac{A_{L_{i-1}}-A_{L_i}}{A_{L_{0}}}=\sin^2({\frac{\pi}{N}}) \cos^{2i-2}(\frac{\pi}{N})
So we just have to find the following infinite series which is a trivial Arithmetic Geometric Progression.
\mathbb{E}[X]=\sum_{i=1}^{\infty} i \times \sin^2({\frac{\pi}{N}}) \cos^{2i-2}(\frac{\pi}{N}) \\
\mathbb{E}[X] \cos^2(\frac{\pi}{N})=\sum_{i=1}^{\infty} i \times \sin^2({\frac{\pi}{N}}) \cos^{2i}(\frac{\pi}{N})
\text{Subtracting both equations.}
\mathbb{E}[X](1-\cos^2(\frac{\pi}{N}))=\sum_{i=1}^{\infty} \sin^2({\frac{\pi}{N}}) \cos^{2i-2}(\frac{\pi}{N}) =\frac{\sin^2(\frac{\pi}{N})}{1-\cos^2(\frac{\pi}{N})}=1 \\
\boxed{\therefore \mathbb{E}[X]=\frac{1}{1-\cos^2(\frac{\pi}{N})}=\cosec^2(\frac{\pi}{N})}
6 Likes
Okkk thanks
Thanks
It was just a GP…
First term = 1
Common ratio = 1/(1-sin^2(theta)))
where theta = (n-2)pi/(2n)
mine code :
#include <bits/stdc++.h>
using namespace std;
#define lli long long int
#define ff first
#define ss second
#define endl ‘\n’
int main()
{
int t;
cin>>t;
while(t–)
{
int n;
cin>>n;
double r = sin(M_PI*(n-2)/(2n));
r=r; // it is r multiplied by r[not visible bcoz of codechef font problem]
double ans= 1/(1-r);
printf("%.8lf",ans);
cout<<endl;
}
return 0;
}
If u hv doubt in any step, u can ask…
Sure, I liked your confidence
1 Like