I’m getting a TLE with this code. Please help!
Are you sure you’ve read the entire editorial? He has explained the DP recurrence pretty well.
A different solution using dp with segment trees.
Updating the last index using two pointers and Updating MEX of current subarray using segment trees rest is trivial prefix sum and dp.
Nice Question. Smart use of multiset.
no need of multiset, can do with arrays and vectors.
Overlapping subproblems is the intuition of DP, and I have mentioned it in video. Which part of the video did you not understand ?
First of all I have read the entire editorial many times and am also not questioning about his explanation. But I just told that the editorial is not detailed.
I have seen many of his video explanations all are good.
I understood it. But was just expecting a proof of the dp intuition. Often a proof makes many doubts clear and also encourages other solutions.
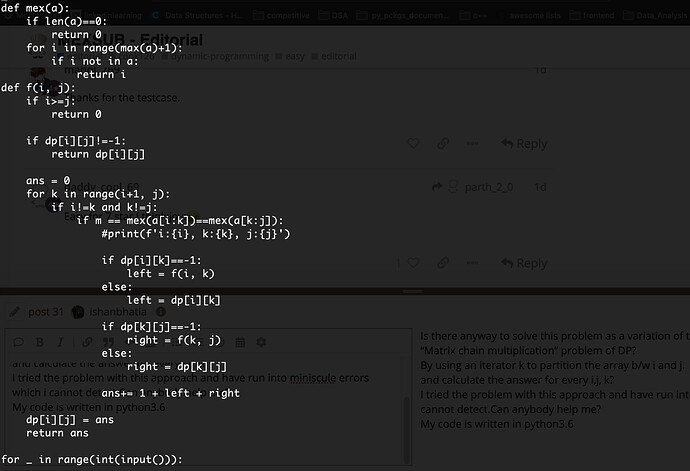
Is there anyway to solve this problem as a variation of the
“Matrix chain multiplication” problem of DP?
By using an iterator k to partition the array b/w i and j.
and calculate the answer for every i,j, k?
I tried the problem with this approach and have run into miniscule errors which i cannot detect.
Can anybody help me?
My code is written in python3.6
def mex(a):
if len(a)==0:
return 0
for i in range(max(a)+1):
if i not in a:
return i
def f(i, j):
if i>=j:
return 0
if dp[i][j]!=-1:
return dp[i][j]
ans = 0
for k in range(i+1, j):
if i!=k and k!=j:
if m == mex(a[i:k])==mex(a[k:j]):
#print(f'i:{i}, k:{k}, j:{j}')
if dp[i][k]==-1:
left = f(i, k)
else:
left = dp[i][k]
if dp[k][j]==-1:
right = f(k, j)
else:
right = dp[k][j]
ans+= 1 + left + right
dp[i][j] = ans
return ans
for _ in range(int(input())):
n = int(input())
a = list(map(int, input().split()))
m = mex(a)
dp = [[-1 for _ in range(n+1)] for _ in range(n+1)]
print(f(0, n))
Can someone post a recursion+memo solution ? Thank you.
what is the intution behind dp[0] = 1 ?
F
how we arrived this formula 2^(n-1) if mex = 0? can anyone explain?
if mex is 0 then we consider all possible sub arrays.
s = {1, 2, 3}
then answers will be
- {1, 2, 3}
- {1, 2} {3}
- {1} {2, 3}
- {1} {2} {3}
I maybe wrong but this is what i understood.