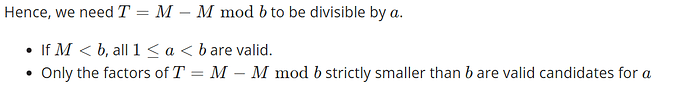One optimization would be to avoid binary search, and just maintain the number of factors already counted and go on taking on from there only to count more factors less than current number.
Also, we don’t need to go beyond M, as if b > M, then M mod b = M and there a would be just b - 1. as any a < b, would satisfy M mod a = (M mod b) mod a = M mod a .
So, time complexity would be M log M + M, so N could be large.
I have seen the approach in editorial and understood it, apart from it i have seen people submitting a code which i couldn’t understand , can someone please help me in this .
Here is the code :
#include <vector>
#include <iostream>
using namespace std;
#define ll long long
int main()
{
ll t;
cin >> t;
while(t-- > 0)
{
ll n,m;
cin >> n >> m;
ll counter=0;
vector<ll> mxn(n+1,1);
for(ll ctr = 2; ctr<=n; ++ctr)
{
ll a = m%ctr;
counter+=mxn[a];
for (ll j=a;j<=n;j+=ctr) {
mxn[j]++;
}
}
cout << counter << endl;
}
return 0;
}
I wanted to understand the underlying logic of this code and proof of why its working. Looking forward to the community: 
So what you’re saying is that you did not understand the approach used in this solution, yet you have an AC solution with this same approach during the contest. Got anything to say?
Link to the solution:
https://www.codechef.com/viewsolution/46261319
I saw this problem ,and find it similar to above. I understood it , but just wanted to get some more insight on it.
Ok then, I’ll try to explain as much as I can. First of all, a counter array of all Mod values is made, i.e. the indexes of the array denote the mod answer. So, with the counter array , you basically are calculating all the pairs that end up at that index and in every iteration, with incrementing a sum value by mxn[a], you’ll be able to sum up all pairs.
Thanks ,can u suggest some similar problems for practise if u have?
As much as I’d love to, I can’t seem to remember any from the top of my head. Sorry man. 
I’ll explain my idea (another approach than editorial) with an example
let N=7 and M=47
say for 2 - (2,3), (2,4), (2,5), (2,6), (2,7) are interested ordered pairs
for each values like this for 1,3,4,5,6 if we find all ordered pairs, this is the brute O(N^2)
how do we optimize it ?
intuition is,
M%a%b == M%b%a
reduce it by fixing the ordered pairs (2,3), (2,4), (2,5), (2,6), (2,7),
M%2%b == M%b%2 (fixing ‘a’ as 2 in our ordered pairs)
LHS :-
since possible values of ‘b’ (3,4,5,6,7) here will always be greater than 2
we can for sure say LHS is to output what M%2 outputs here, which is M%2 = 47%2 = 1
why ?
0%(3 or 4 or 5 or 6 or 7) gives 0 always
1%(3 or 4 or 5 or 6 or 7) gives 1 always
RHS :-
now problem reduces to, we need RHS to match LHS’s value 1,
i.e. (M%b)%2 = 1 what are the possible values of ‘b’ which can give me this output
if M%b outputs 1, 3, 5 (bounded by N=7, as values >= 7 are not possible remainders)
(1 or 3 or 5)%2 = 1 in all cases which matches our LHS
so we can achieve this by having a track of all our M%x count, where 1<=x<=N candidates for a,b
note 1 : while counting we should reduce one count for M%b%2 where (M%b) is 1 as we seek values of b greater than 2 ie. 3,4,5,6,7 which gives remainders 1,3,5,7
note 2 : once done with ordered pairs fixed a=2 we reduce the count in the mod table for M%a = M%2 = 47%2 = 1 so that it doesn’t affect further ordered pairs
Time complexity is O(N * log(N))
for each [1-N] we do log(N) operation
how log(N) ? ans since we do 1 + 1/2 + 1/3 + … + 1/N ~ log(N) operations
private long solution(int N, int M) {
int[] mod_table = new int[N];
for (int i=1;i<=N;i++) {
mod_table[M%i]++;
}
long count = 0;
for (int i=1;i<=N;i++) {
int val = M%i;
mod_table[val]--;
for (int j=val;j<N;j=j+i) {
count += mod_table[j];
}
}
return count;
}
Bro can u explain in a bit more detail… I am unable to get it.
Someone pls tell why we are writing : M = b * [M/b] + M mod b
Can you explain i more detail
About where the main condition ((M%a)%b)=((M%b)%a)) is check in above code and when the second for will exit
suppose m=13 and b=5
now [m/b] is nothing but the quotient m/b=2
[m%b] is the remainder m%b=3
b is the divisor b=5
m is dividend m=13
We r just applying this maths equation
dividend=(divisor*quotient+remainder)
How does the sieve method cost O(M * log(M)).??
till here i understood. How we are going to use this equation while writing code?
This problem instantly reminded me of this problem.
Obviously they’re very different(or close 
).
After that just store the factors of all numbers from 1 to M (using the sieve fashion shown in editorial) and then whenever u face (M-Mod b) we know the factors already so binary search on them to get number of factors less than b.
I don’t think there was any need to represent M-Modb as b*(M/b) as such in this .
Bro can You Explain in detail ‘Here’’
int val = M%i;
mod_table[val]--;
for (int j=val;j<N;j=j+i) {
count += mod_table[j];
}
Anyone please explain How this code works. The time taken for this code is 0.02 sec.This is the code link CodeChef: Practical coding for everyone . I have code as per the editorial(youtube) but the time is 0.63. . Thanks in Advance.
how ((M mod b)mod a)= M mod a?
