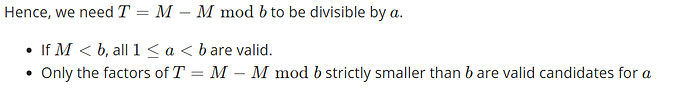I’ll explain my idea (another approach than editorial) with an example
let N=7 and M=47
say for 2 - (2,3), (2,4), (2,5), (2,6), (2,7) are interested ordered pairs
for each values like this for 1,3,4,5,6 if we find all ordered pairs, this is the brute O(N^2)
how do we optimize it ?
intuition is,
M%a%b == M%b%a
reduce it by fixing the ordered pairs (2,3), (2,4), (2,5), (2,6), (2,7),
M%2%b == M%b%2 (fixing ‘a’ as 2 in our ordered pairs)
LHS :-
since possible values of ‘b’ (3,4,5,6,7) here will always be greater than 2
we can for sure say LHS is to output what M%2 outputs here, which is M%2 = 47%2 = 1
why ?
0%(3 or 4 or 5 or 6 or 7) gives 0 always
1%(3 or 4 or 5 or 6 or 7) gives 1 always
RHS :-
now problem reduces to, we need RHS to match LHS’s value 1,
i.e. (M%b)%2 = 1 what are the possible values of ‘b’ which can give me this output
if M%b outputs 1, 3, 5 (bounded by N=7, as values >= 7 are not possible remainders)
(1 or 3 or 5)%2 = 1 in all cases which matches our LHS
so we can achieve this by having a track of all our M%x count, where 1<=x<=N candidates for a,b
note 1 : while counting we should reduce one count for M%b%2 where (M%b) is 1 as we seek values of b greater than 2 ie. 3,4,5,6,7 which gives remainders 1,3,5,7
note 2 : once done with ordered pairs fixed a=2 we reduce the count in the mod table for M%a = M%2 = 47%2 = 1 so that it doesn’t affect further ordered pairs
Time complexity is O(N * log(N))
for each [1-N] we do log(N) operation
how log(N) ? ans since we do 1 + 1/2 + 1/3 + … + 1/N ~ log(N) operations
private long solution(int N, int M) {
int[] mod_table = new int[N];
for (int i=1;i<=N;i++) {
mod_table[M%i]++;
}
long count = 0;
for (int i=1;i<=N;i++) {
int val = M%i;
mod_table[val]--;
for (int j=val;j<N;j=j+i) {
count += mod_table[j];
}
}
return count;
}
 .
.