Cool. Neglecting the time taken by UFDS, still, the time complexity is O(N\log{N}), isn’t it a bit too high for given constraints (10^7)?
Sieve of Eratosthenes is O(N.log(log(N))), and can also be made linear. Also, your prime factorisation is very fast because only perfect powers of two have log2(x) factors.
All this combined with the fact that your code has a very good constant factor is good enough to get 100 points here.
Nice explanation. Thank you for taking the time to explain this. 
In order to make work for corner cases you changed the solution. ( the loop should be from [n/2+1 to n]
https://www.codechef.com/viewsolution/47286411
Here see changes. It gives TLE u have to use prefix sum. n=10^7
Also in sieve I think we should put (ll)i*i<=n to prevent overflow, which will make sieve work correctly for larger i.
I have figured out the whole approach during the contest. I also know the concept of sieve, yet my solution was giving segmentation fault at contest time. But my solution is exactly the same as editorialist. I don’t know why his solution accepted but not mine. Can you help? plz.
#include<bits/stdc++.h>
using namespace std;
#define ll long long int
const int max_size = 1e7 + 1;
int primes[max_size];
void sieve()
{
for (int i = 2; i < max_size; i++)
{
if (primes[i])
{
for (ll j = i * i; j < max_size; j += i)
{
primes[j] = 0;
}
}
}
for (int i = 3; i < max_size; i++)
{
primes[i] += primes[i - 1];
}
}
void solve()
{
int n;
cin >> n;
int ans = primes[n] - primes[n / 2] + 1;
cout << ans << endl;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
for (int i = 1; i < max_size; i++)
primes[i] = 1;
sieve();
int t;
cin >> t;
while (t–)
solve();
return 0;
}
Yes you are right, thanks, I might have not figured it myself
I also used linear sieve , getting TLE , can you please tell where i am getting wrong
Here is the code.
I also used linear sieve , getting TLE , can you please tell where I am getting wrong
Here is the code.
The Time complexity of your code is O(N) per test case. Optimise it further, like storing the values somewhere.
you don’t need to call your sieve function again and again , we are using it for pre-computation so we will just declare it before taking t, also the lp array calculation must be done in the sieve function, I have made some changes with your code and your accepted code is here ![]()
@king_rayuga
can you please tell me why my code is giving tle for 2nd subtask
code link
thank you in advance
so you have to precalculate the sieve function so make a separate function and calculate for n = 1e7 and call it before taking t, and you are taking 0(n) time per test case which is not ideal, it should be either O(1) or O(log(n)) per test case, so try to precalculate your ‘arr’ array and find a way such that per test case time complexity is O(1) or O(log(n)),
Ok , my code was calling sieve again for all the test cases , and that’s the shit in my code , Thanks.
I am getting TLE in subtask 2. Can anyone Help!!!
public static void main (String[] args) throws java.lang.Exception
{
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(bf.readLine());
while(t-- > 0)
{
int n = Integer.parseInt(bf.readLine());
boolean num[] = new boolean[n+1];
Arrays.fill(num,true);
num[0] = num[1] = false;
//Initialization Done
for(int i = 3 ; i*i <= n ; i+=2)
{
//If "i" is not prime then skip
if(!num[i])
continue;
//if i is prime then go to next multiple of i
int temp = i*2;
//make FALSE to all value which are multiple of i
while(temp <= n)
{
num[temp] = false;
temp += i;
}
}
int grp = 0;
for(int i = 3 ; i <= n ; i+=2)
{
//if num is prime and greater than n/2
if( num[i] && i > n/2)
grp++;
}
System.out.println(1+grp);
}
}@rathod_009
even i was getting tle for subtask 2 and i just discussed this and got a answer
what you are doing is calculated sieve for every test case and also calculated number of prime numbers till n and calculated number of prime numbers till n/2 for every test case
even i did the same and hence got tle
instead we can only calculate it once that is before while(t–>0) and store it and then use it with time complexity O(1)
note:also see the ans posted by king_rayuga
You need to precompute the primes and prefix of primes before executing any test case. Precompute for n= 10^7 before you start the while(t–) loop. Refer to my solution CodeChef: Practical coding for everyone
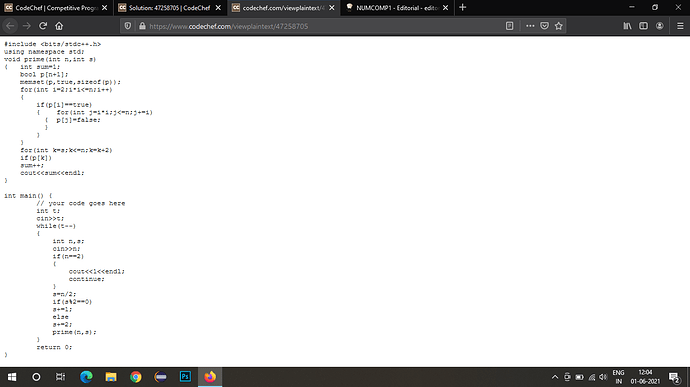
Can anybody tell me why my solution to this problem (NUMCOMP1) is showing TLE error for subtask2?
Here is my code:
#include <bits/stdc++.h>
using namespace std;
void sieve(int n)
{
int count = 0;
bool prime[n + 1];
memset(prime, true, sizeof(prime));
for (int p = 2; p * p <= n; p++)
{
if (prime[p] == true)
{
for (int i = p * p; i <= n; i += p)
prime[i] = false;
}
}
for (int p = n/2+1; p <= n; p++){
if (prime[p]){
count++;
}
}
cout << count+1 << endl;
}
int main()
{
int t;
cin >> t;
while(t–){
int m;
cin >> m;
if(m == 2) cout << 1 << endl;
else if(m == 3) cout << 2 << endl;
else sieve(m);
}
return 0;
}
gotcha !! thanks mate…