Just for the sake of completeness and helping my fellow buddies. Answer to Q-5 and Q6 are:

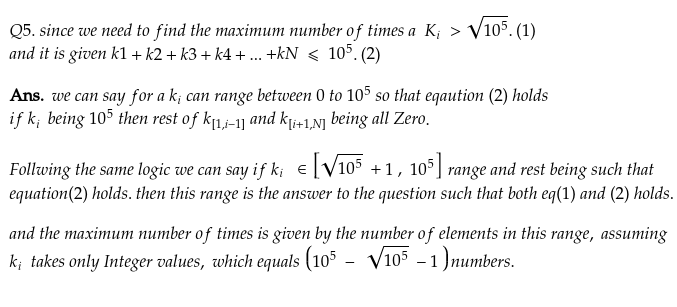
let me know if i am wrong somewhere.

Just for the sake of completeness and helping my fellow buddies. Answer to Q-5 and Q6 are:

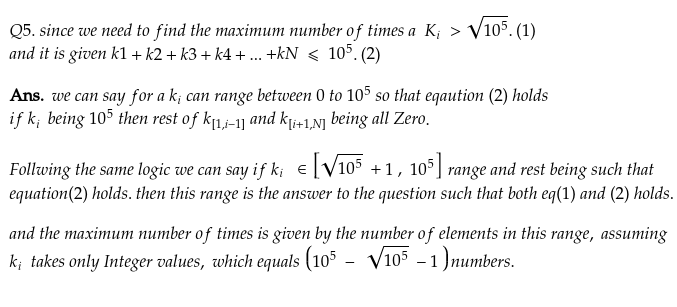
let me know if i am wrong somewhere.

Umm, sure. So the ones I recommended are Vim, Gedit, Nano, Emacs. Out of these if you look up on the net most productive ones are generally said to be Vim/Emacs. Along with this one would need to get comfortable in terminal and use g++/gcc from terminal along with basic file redirection and piping.
Q6 your answer and justification are correct.
For Q5, I was trying to ask a different question, maybe my phrasing was bad. The thing I wanted to test was, how many different K_is can there be with value greater than sqrt(10^5) and the answer would simply be at most sqrt(10^5). Because if one has more than sqrt(10^5) K_i’s each with value >= sqrt(10^5), then the sum of these K_i’s > sqrt(10^5) * sqrt(10^5) = 10^5, which contradicts the fact that sum of all K_i’s = 10^5
Yes then N should be sqrt(10^5). Also since u asked k> sqrt(10^5) and not equal to. So even if one of the value is sqrt (10^5)+1 ,then all rest of them must be
less than sqrt(10^5).
I have a doubt in Multiple of three problem . For the test case :-
1
2 3 4
The correct answer should be NO because the number should be 34 and it’s sum is 7 so, it should not be divisible by 3 . But most of the correct solutions to this problem are showing YES . can anyone explain why ?
here’s my solution:-
https://www.codechef.com/viewsolution/31303740
it was a very nice session, it will be helpful for learning
Please help me to solve MULTHREE my answer is not coming
The youtube video isn’t present now.
The Youtube Video is private now and we cannot access it. Can you please make it public again. It would be really helpful. Thanks!
Yes, Please make the video public.
A great effort by the CodeChef Team.
I joined the contest a little late.
Could you please give me access to the youtube video of the Contest 1-Part1 Discussions.
Yes, we have taken down the video due to certain issues with the content. We are fixing it and will be making it live within a couple of days.
I’m not able to understand why I’m getting wrong answer for my submission. Following is the link to my submission:
https://www.codechef.com/viewsolution/33043153
@sidhant007
In question 3,
the no. of numbers with last digit as 0 are 2^(p-1);
the no. of numbers with last digits as 01 are 2^(p-2);
but the thing is the no of operations required for the numbers with last digits 01 is 2.
So the overall complexity should be 1*(2^(p-1))+2*(2^(p-2))+3*(2^(p-3))…
The complexity will be Big_SIgma(N) and will be greater than O(N).
Please correct me if wrong.
@sidhant007
I have a doubt in the solution of question MULTHREE.
The below is my implementation of calculatiing the left part of the total.
Here the variable left_over is calculating the total left over part to be added and the variable left_over_count has calculated the number of digits left over after the first three digits and cycles.
int left_over;
if (left_over_count == 1)
{
left_over = (2 * x) % 10;
}
if (left_over_count == 2)
{
left_over = ((4 * x) % 10) + ((2 * x) % 10);
}
if (left_over_count == 3)
{
left_over = ((8 * x) % 10) + ((4 * x) % 10) + ((2 * x) % 10);
}
I dont understand what’s wrong in my implementation. After copying your in place of that my solution came right. I tried to print the digits given by it and matched with the two test cases it were same.
Errichto dropped a video on the topic of why we do modulo by a specific number 10^9+7 on online judges, have a look. Computations Modulo P in Competitive Programming - YouTube
Ummm @elon_musk10 your analysis is partially correct, I have fixed and put it in the comments on the youtube channel.
Copy pasting that comment here:
Fix: The analysis is actually \sum_{i = 1}^{P} 2^{P - i} * i (Notice you need to multiply with i, because the increment function takes i steps for those x’s)
Let S = \sum_{i = 1}^{P} 2^{P - i} * i = (2^{P - 1})*1 + (2^{P - 2})*2 + \dots + (2^1)*(P - 1) + (2^0)*P
Then 2S = (2^P)*1 + (2^{P - 1})*2 + (2^{P - 2})*3 + \dots + (2^1)*P
So 2S - S = 2^P + 2^{P - 1} + ... + 2^1 - (2^0)*P = (2^{P + 1} - 1) - P \leq 2 * 2^P \leq 2*N
So S = O(N)
Factorial Question in Contest 1: CodeChef: Practical coding for everyone
Can someone help me what’s wrong in my approach here : https://www.codechef.com/viewsolution/33535115
Thanks.