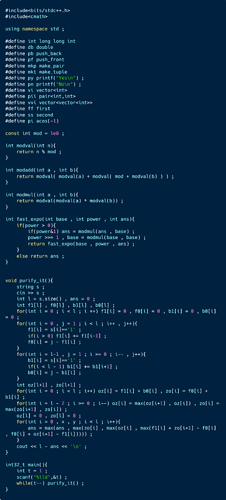
Bro, have a look at my solution, i solved it on first go as my approach is extremely simple to implement
Look at my solution, it is really very simple dp approach :
here is the O(n) approach .
in this case we have to find maximum length of 101 / 010 / 10 / 01 / 1 / 0 as a subsequence
so in this case we have to find length of subsequence where all characters are 1 and 0 ,
then we have to store length of 10 / 01 as subsequence means(000111 / 1111100 like this)
but we have to store maximum length of oz[i](one , zero) so that we can get maximum length of 101 and similarly for 010 subsequence , so for that we we store maximum of oz[i] from by traversing from (l-2 to 0)(where l is length of string) we traversing backward because 01 / 10 will append in subsequence 101 / 010 as suffix ,
and last of all , to find 101 we will add number of 1’s upto index i + maxmimum length of subsequence 01 since it will inclde zeroes upto index i so we have to exclude that , same for 010 also .
so in this way we find our ans