Well, damn. My AC code outputs
YES
k2
k3
k1
I used topological sorting with Kahn’s algorithm.The indegree of nodes k2 and k3 and 0 initially. After removing them, the indegree of 1 becomes 0. So my code outputs “YES” along with that order.
My code:
#include <bits/stdc++.h>
using namespace std;
const int size = 1e2+1;
vector <int> adj[size];
vector <int> res;
vector <int> in(size);
void kahn(int n)
{
priority_queue <int, vector <int>, greater <int>> pq;
for (int i = 1; i <= n; ++i) if (in[i] == 0) pq.push(i);
while (!pq.empty())
{
int curr = pq.top();
res.push_back(curr);
pq.pop();
for (int child : adj[curr])
{
in[child]--;
if (in[child] == 0)
pq.push(child);
}
}
if (res.size() != n) cout << "NO\n";
else {
cout << "YES\n";
for (int i : res)
{
string ans = "k";
ans.append(to_string(i));
cout << ans << '\n';
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while (t--)
{
int n, m;
string u, v;
cin >> n;
cin >> m;
for (int i = 0; i < m; ++i)
{
cin >> u >> v;
adj[stoi(v.substr(1, v.size()-1))].push_back(stoi(u.substr(1, u.size()-1)));
in[stoi(u.substr(1, u.size()-1))]++;
}
kahn(n);
res.clear();
for (int i = 0; i < size; ++i) adj[i].clear();
in.clear();
in.resize(size);
}
}
Will adding Kosaraju’s or Tarjan’s algorithm for finding the number of strongly connected components work? Becasue from my observations of the sample testcases, the answer was “NO” only when the number of strongly connected components exceeded 1 (and you cannot perform topological sort). Someone please let me know about this.
And @rakshi20_20, thanks a lot for pointing this out. Gotta improve my solution now  .
.
1 Like
I don’t really understand the inputs in the problem.
Consider the input-
6
9
k2 k1
k3 k2
k4 k3
k4 k6
k5 k4
k1 k5
k2 k1
k6 k4
k4 k6
How can k6 win in one round against k4 and in another k4?
This test case doesn’t follows what the problem statement says.
1 Like
I will tell what I did-
It is pretty straightforward.
Consider the test case-
4
7
k1 k2
k1 k2
k2 k3
k1 k3
k2 k3
k3 k4
k1 k4
Consider the first column as list-1 and second as list-2. I’m first assuming that a valid unique permutation exists such that all above requirements are satisfied.
Observe that k4 is not present in list-1. This suggests that k4 has least power as it didn’t win any competition(I have assumed that a unique valid permutation exists and till now no constraint has been broken). So, till now arr = [k4].
I will remove the fights where k4 is involved as now I know the exact place of k4.
Fights reduce to-
k1 k2
k1 k2
k2 k3
k1 k3
k2 k3
Now, repeat the same thing and append k3 to arr. So, arr = [k4, k3]
…
Repeating till we get a valid permutation - arr= [k4, k3, k2, k1]
What are the conditions when the ans will be **No**?
At any stage (before we get valid permutation, if possible),
- If there this no one (out of remaining people which are yet to be placed in
arr) which is not present in list-1 (or simply everyone is present) that means the input is invalid. Ideally, this case should not occur according to problem statement but the problem has an input (input-2) where it occurs. I’d consider that input incorrect. Thus, if input is incorrect, no valid permutation would exist.
- If there are more than 1 persons which are not in list-1 means we can’t conclude and multiple valid permutations may satisfy the constraints. There is no unique answer. So, we’ll output No.
Code in Python3
t=int(input())
for _ in range(t):
n = int(input())
m = int(input())
arr=[]
for i in range(m):
a,b=input().split()
arr.append((int(a[1:]),int(b[1:])))
ans=[]
tot=[x for x in range(1,n+1)]
while True:
if len(ans)==n:
break
d={}
for i in arr:
if i[1] not in ans:
d[i[0]]=1
ele=list(set(tot)-set(d.keys()).union(set(ans)))
if len(ele)!=1:
ans = "NO"
break
ans.append(ele[0])
if ans=="NO":
print(ans)
else:
print("YES")
for i in ans:
print('k'+str(i))
1 Like
yeah i think we have to just print topological order. According to the question k4 and k6 can not win to each other at the same time.
But if we consider the topological order then there will be a cycle
between k4 and k6 so i think test cases are made according to the topological order but not considering the question stated.
There is fault in the test cases
1 Like
Yes…It is indeed topological sorting.
TS doesn’t exist if it is not a DAG.
So, yeah, second input forms a cycle…so, no valid TS permutation as I explained above.
If for any input TS exists, it should be unique else answer will be No.
2 Likes
Thanks for the solution…maybe those which I saw somehow managed to pass testcases . Anyways thanks for providing 
@anon53253486 yeah…I ,too, need to improve my WA solution 
I did topological sorting using a queue but every time a node was pushed to queue,I was checking if only a single node had in-degree==0 which means it’s the highest (orderwise) among all left. But this gave me WA,any ideas why it fails ?
Can you attack the relevant code? I’ll reply in some time.
editorials for all the sums will be out soon
Hi,
As mentioned in the last line of the problem statement. “There will always be a unique answer to each test case”
So you won’t get such inputs while testing. The only cases the answer should be no are the ones where ranks cannot be determined i.e. the graph formed is cyclic.
1 Like
@vedant_k07 What is the approach for last problem
1 Like
hey!! can anyone check why my code gives WA
- I check first graph is cyclic or not if it is cyclic than answer is no
- topological sort using kahn algo printing yes
CodeChef: Practical coding for everyone
Many users have mentioned using topological sorting to solve this problem, I used a slightly different approach.
firstly i tried to calculate all the possible deduction i can make based on the give fight results, for which i used a set and used the condition that if for two pairs {p1,p2} and {p2,p3}, then {p1,p3} is also a pair. I kept on adding pairs of these kinds untill i could, and then used simple logic that the most powerful knight shoul defeat all other n knight and thus should apperar n-1 time as the first element, similarly for all the other knights also.
link to my code
You just need to check if the number of nodes in the queue are greater than 1 at any time. If so, the answer is “NO” because multiple topological sorts will exist.
The code is:
#include <bits/stdc++.h>
using namespace std;
const int size = 1e2+1;
vector <int> adj[size];
vector <int> res;
vector <int> in(size);
void kahn(int n)
{
priority_queue <int, vector <int>, greater <int>> pq;
for (int i = 1; i <= n; ++i) if (in[i] == 0) pq.push(i);
while (!pq.empty())
{
if (pq.size() > 1) break;
int curr = pq.top();
res.push_back(curr);
pq.pop();
for (int child : adj[curr])
{
in[child]--;
if (in[child] == 0)
pq.push(child);
}
}
if (res.size() != n) cout << "NO\n";
else {
cout << "YES\n";
for (int i : res)
{
string ans = "k";
ans.append(to_string(i));
cout << ans << '\n';
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while (t--)
{
int n, m;
string u, v;
cin >> n;
cin >> m;
for (int i = 0; i < m; ++i)
{
cin >> u >> v;
adj[stoi(v.substr(1, v.size()-1))].push_back(stoi(u.substr(1, u.size()-1)));
in[stoi(u.substr(1, u.size()-1))]++;
}
kahn(n);
res.clear();
for (int i = 0; i < size; ++i) adj[i].clear();
in.clear();
in.resize(size);
}
}
Topological sort suffices for this problem. Very simple! 
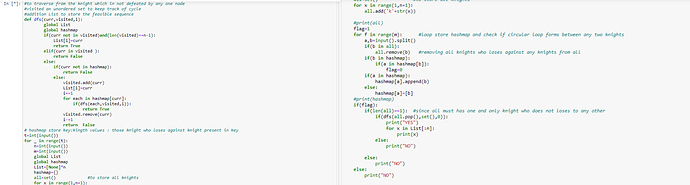
hello coders ,need your suggestion and review .
here goes my documented code in python3.
will be waiting for review.
in case any thing in ambiguous or unclear,plz let me know
happy coding.
Bro,I tried to do the same thing …can you please have a look at my code and tell where is it going wrong .
https://www.codechef.com/viewsolution/33616776
Hi,
We will share the editorial by the end of the day
2 Likes
 .
.