Understood! Thanks ![]()
Can you explain this part ?
OK straight to the point. The answer is either:
- -1 this can be checked easily
- The minimum time if we can find 2 different minimum time paths
- The answer can be minimum time + 2 understandable just do a jaywalk
Question: Give me a proof that it can never be minimum time + 1. Don’t just say, “not possible”. OK intuitively it seems not possible. I didn’t found any case where it is possible but I want a certain black and white reason.
As in case of t+2 , the robot 2 follows shortest path of robot 1 but they wont reach n,m simultaneously right . But in the question it has been mentioned .
Can you explain what was the issue with the solution? Is it wrong or something?
I don’t have a solid reasoning but you can think of it in this way , let’s say you are starting at (1,1) and want to reach cell (N,M) , so obviously , each step you want to take is towards your goal , that is for the shortest path , you would want to take total (N - 1) down steps and (M - 1) right steps , resulting in (N + M - 2) steps. Let’s say at any point of time this path is blocked by the cell ‘#’ , then essentially , you can’t take a right or down step and are forced to take a step towards the left or up (away from your target) , each of this step is forced to be compensated with a step in the opposite direction at some instance of time , that is , if you take a step towards the left , then you are forced to go right at some point (resulting in an addition of 2 steps and not 1) , so the parity of the length of the SHORTEST paths from the source to destination never changes , that is lets say we were to figure out what are the K shortest path lengths from (1,1) to (N,M) , then all the numbers in there would have the same parity…(I hope I am clear)
Now , can someone help ME with my problem , like my logic was the same , if we find 2 shortest paths , then answer is their length , else its their length + 2 , although it seems the way i check if there exists multiple shortest paths is wrong , what i did was find one shortest path and all the elements along the path , and if at any instant , i reach any of the cell in that path in the same time through a different path , then my job is done , else its not , Here’s my code , pls lmk if u find any test case that’s going wrong or any flaw in the logic itself…
https://www.codechef.com/viewsolution/1125174725
That’s not a proof. That is called intuition which is not always correct(but I wish).
Proof: A grid(with no non-linear jump) is a bipartite graph(proof: chromatic number 2). So each vertex belongs to either of 2 different sets. Let’s color them black and white(resembling a chess board). So you have 2 sets like so:
Set A (only white color nodes) and Set B (only black color nodes).
Consider this case: Going from black node to white node with distance x. So any other route from node black to white has to go to Set B and then back to Set A(because same set have no edges in bipartite graph) and any odd length like x+1, x+3, x+5 means that we travelled in the same set which is not possible in bipartite graph so minimum we have to switch the set and then come back which is nothing but 2 operations and can only be 2*n
Take all other cases Black to White, Black to Black, White to Black, White to White and verify that its always 2*n.
So from minimum the answer can only increase by 2.
Key observation: Given grid is a planar Bipartite graph
Too deep for me , i need to clear a bit more concepts before the proof starts making sense to me…
They do enter simultaneously. First R1 reaches at T then at T+1 moves to some adjacent square, then both are 1 square away from reaching (n,m). Then, both of them come to (n,m) at T+2
Help me with this -
Why are we checking for this -
if(grid[0][1] == ‘#’ || grid[1][0] == ‘#’ || grid[n-1][m-2] == ‘#’ || grid[n-2][m-1] == ‘#’) for unavailability of path.
Instead of this -
if(grid[0][1] == ‘#’ || grid[1][0] == ‘#’ || (grid[n-1][m-2] == ‘#’ && grid[n-2][m-1] == ‘#’))
Let’s consider a case -
n = 3 m = 3;
grid = . . #
. # #
. . .
In this case, the answer should be 6, the robot 1 will follow the path of - (0,0)->(1,0)->(2,0)->(2,1)->(2,2) and robot 2 will follow - (0,0)->(1,0)->(0,0)->(1,0)->(2,0)->(2,1)->(2,2) so the answer should be 6 in this case. But the solution its accepting returns -1 for this case.
We should only have to check for the starting position because on the first time we move, the robots should be on different cells but for destination we have to check for at least an adjacent open cell of destination cell.
Hello.
I think the way used by the Author’s code to greedily find two non-intersecting shortest paths might be incorrect.
You can check the issue using the following test:
1
7 8
....####
.##.####
..#.####
#.#.#...
......#.
.######.
........
The expected answer should be 15 as it is possible to find two non-intersecting shortest paths (see picture below).
Instead the author’s code outputs 17. That’s because the code constructs
- the first path (green) by always moving upward. And if not possible it moves, in order, toward the left, toward the right and finally downwards.
- the second path (red) by always moving downward. And if not possible it moves, in order, toward the right of the grid, toward the left and finally upward.
For this reason, the two shortest paths computed by the code intersect.
Expected VS obtained paths
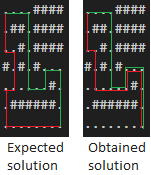
I suppose one possible way to fix the issue would be to navigate the grid “in first person” like a maze and construct the first path by “always turning at your left” and the second path by “always turning at your right”.
I hope I didn’t miss anything and I was able to give you an idea of the issue and possible fix. I’m willing to elaborate if required.
Yes, the authors code is wrong.
But I think it can easily be fixed by the following:
- the first path (green) by always moving upward. And if not possible it moves, in order, toward the left, toward the right and finally downwards.
- the second path (red) by always moving downward. And if not possible it moves, in order, toward the left of the grid, toward the right and finally upward.
Can someone debunk my solution?
https://www.codechef.com/viewsolution/1125655635
I think the testcases are incorrect for this question, the part of having both grids next (n,m) empty seems incorrect as there still maybe a path.
Example:
3 3
…
…
##.
Correct output: 6
Submission output: -1
I made the following submission Submission#1126180978 with the following snippet added and it gets accepted.
if (grid[n - 2][m - 1] == '#' || grid[n - 1][m - 2] == '#') {
cout << "-1\n";
return;
}
You are not understanding the problem , it says that the robot need to reach simultaneously , so when the correct output is -1 and not 6 , because if the 1st robot reaches (3 , 3) at that instant the robot 2 should be at (2 , 2) or (3 , 1) , but in either of the cases , the robot1 would have no square and would be forced back to (2 , 3) and since robot 2 wants to chose the optimal path as well , it would come to (2 ,3) as well , which contradicts the problem statement , as it mentions that both robots should not be on same square except for (n , m) , so as a conclusion there should always be a spare(waiting) square for robot 1 in case robot 2 does not have a disjoint shortest path to (n , m). I hope you understand , else we can discuss more over this.
The answer can’t be 6 , check the bottom most comment , i just replied to some other user who addressed the same issue.
The problem says the have to be “at (N,M) simultaneously” not “reach simultaneously”.
From the above editorial when answer is (T+2):
Otherwise, robot 1 can follow the shortest path, while robot 2 can first move away from (1, 1) to the other cell, then move back to (1, 1), and then follow the shortest path
This also implies that they do not have to reach simultaneously.
You are still missing the point, the problem does say that they have to REACH at (N,M) simultaneously and not be there simultaneously. The answer can be T + 2 because when the first robot reaches it at time = T, the second robot is still 2 steps away from (N, M) and now the robot 1 plays a waiting move while robo 2 takes a step towards (N, M) , at this instant time = T + 1 . And exactly at time = T + 2 , both the robots REACH the destination simultaneously.
the problem does say that they have to REACH at (N,M) simultaneously and not be there simultaneously
The question literally says “be at (N,M) simultaneously”:
Your goal is to find the minimum time needed for both the robots to be at (N,M) simultaneously.
On further retrospection I found out that it is not possible for them to arrive out of sync, so in this case being their simultaneously also means reaching there at the same time.