Can anyone plz explain me how to solve this problem…I’m relatively new to Competitive Programming,
Snow Walking Robot- https://codeforces.com/contest/1272/problem/B
Editorial Link- Codeforces Round #605 (Div. 3) Editorial - Codeforces
I tried going through the editorial but still can’t get it:frowning_face:
Also, if this problem needs some knowledge of advanced topics plz tell me about those as well.
Thanks for the help!
you don’t need knowledge about any advanced topic for this one, logical thinking is enough. Basically you need to start from the origin and end back there without revisiting any cell. That requires your displacement in x-direction and y-direction to be zero. So we must have an equal number of ‘L’ s and ‘R’ s and similarly an equal number of ‘U’ s and ‘D’ s. You can obtain this by removing the excess elements from the given input string. A greedy solution then will be to go as far LEFT as possible, then as far UP, RIGHT and then DOWN. ( you make a round trip without revisiting any cell (other than the origin at the end)). But be wary of the corner cases where you have non zero ‘L’ s and ‘R’ s and ‘U’ s and ‘D’ s are zero (or the other way around), in this case, the answer will be LR (UD for the other way around), this is to prevent revisiting.
you can take a look at my submission for reference Submission #66713578 - Codeforces
Wow! Thanks a lot!!
Just check out the code, hope, it’s would be easy to you.
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define sz(a) a.size()
#define all(a) a.begin(), a.end()
#define w(a) std::cerr << #a << " : " << (a) << "\n";
bool solve() {
string s;
cin >> s;
if (sz(s) == 1) return cout << 0 << "\n", 0;
int up = 0, down = 0, left = 0, right = 0;
for (const auto ch : s) {
if (ch == 'U')
up++;
else if (ch == 'D')
down++;
else if (ch == 'L')
left++;
else if (ch == 'R')
right++;
}
int up_down = min(up, down);
int left_right = min(left, right);
ll ans = up_down * 2 + left_right * 2;
if (up_down + left_right == 0) return cout << 0 << "\n", 0;
if (up_down == 0) return cout << 2 << "\nLR\n", 0;
if (left_right == 0) return cout << 2 << "\nUD\n", 0;
cout << ans << '\n';
for (register int i = 0; i < up_down; i++) cout << 'U';
for (register int i = 0; i < left_right; i++) cout << 'L';
for (register int i = 0; i < up_down; i++) cout << 'D';
for (register int i = 0; i < left_right; i++) cout << 'R';
return cout << "\n", 0;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
#endif
register int tc;
cin >> tc;
while (tc--) solve();
return 0;
}
Can you explain your solution in detail ?
@kaaaaran12 Sure 
tl;dr
- If length of given string = 1, then answer must be 0 because robot needs at least one more step to get back to home, i.e.
if (sz(s) == 1) return cout << 0 << "\n", 0; - Robot can go n steps UP if it have n down steps. Because robot must get back to home at last.
Therefor robot can go min(up,down) steps up and then down (or vice-versa) BUT there must have min(left,right) steps \ge1 because if there is no left steps, then robot can’t go right (because it can’t back to home). If left or right steps = 0, then robot can’t go more than one step up/down, because it can’t visit one cell more than one time (except home).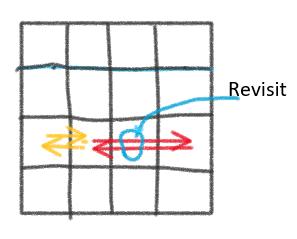
More specifically, If there is no up/down steps, then it can’t move left/right more than one steps, because robot can’t revisit one cell except home. similar for left/right.
.
Code explanation
- If length of string is 1, answer must be zero i.e.
if (sz(s) == 1) return cout << 0 << "\n", 0; - now count up, down, left, right steps in the given string (say s).
Code example:
int up = 0, down = 0, left = 0, right = 0;
for (const auto ch : s) {
if (ch == 'U')
up++;
else if (ch == 'D')
down++;
else if (ch == 'L')
left++;
else if (ch == 'R')
right++;
}
- How many steps robot can go up/down is the min(up,down) i.e.
int up_down = min(up, down);
similar for left/right, i.e.int left_right = min(left, right); - How many steps robot can move = up_down + up_down + left_right + left_right. (counted twice, because it’s 1st up ^1 and then down ^2, similar for left right). i.e.
ll ans = up_down * 2 + left_right * 2; - If there is no up and right steps (BUT have too many left and down steps ) or vice-versa, then it can’t move. i.e.
if (up_down + left_right == 0) return cout << 0 << "\n", 0; - If up/down is zero, BUT have many left and right steps, then it can mode only 2 steps (Home and left/right one), Check out attached image for details. Similar for left/right. i.e.
if (up_down == 0) return cout << 2 << "\nLR\n", 0;
if (left_right == 0) return cout << 2 << "\nUD\n", 0; - Corner cases return the function BUT for general case, we should print out the maximum steps robot can move (calculated before). i.e.
cout << ans << '\n';
Now print out the steps in your preferred order, Here is mine, first up steps, then left, then down then right and hence every cell visited only once (except home). Printout example:
for (register int i = 0; i < up_down; i++) cout << 'U';
for (register int i = 0; i < left_right; i++) cout << 'L';
for (register int i = 0; i < up_down; i++) cout << 'D';
for (register int i = 0; i < left_right; i++) cout << 'R';
return cout << "\n", 0;
Hope it’s clear now. Happy coding 