is don’t open this kept to trigger everyone to open it XD
TEST_CASE
1
3 3 2
1 1
3 3
1 2
2 1
2 3
3 1
1 3
3 2
2 2
Correct output should be Alice your code outputs a Draw
Thanks a lot !
My expression of calculating the prefix sum had a very small bug which i dont know why didn’t strike me ![]()
But yes, It did pass anyways.
Wanted to ask if you find the test cases manually, or create the generator files / other methods…?
Can anyone submit this code of Hidden cell problem from lunchtime, when I m submitting it’s showing internal error and let me know the Verdict if possible.
Link :- CodeChef: Practical coding for everyone
My very optimized O(n*m square) using two pointers for both horizontal and vertical direction, passed almost all test cases except 3 : CodeChef: Practical coding for everyone
my solution dp + binary search
check any kk submatrix exist in NM matrix or not with binary search
https://www.codechef.com/viewsolution/48229268
can you explain or provide resources how 2d sliding window works
super sus bro , filthy cheaters , all have the same solution
Weird verdict ![]() can someone help me where is the error
can someone help me where is the error
The solution uses sliding window kind of algorithm.
TLE code: Submission
AC code: Submission
Magic (Added 2 lines)
#pragma GCC optimize ("Ofast")
#pragma GCC target ("avx2")
It improved my TL by more than 500ms. :dead:
Yes, I wrote a generator and stress-tested my solution against yours. Here’s the generator for anyone interested → gen.cpp
Got it !
Thanks 
Solution without Binary Search or Sparse Table/Segment Tree
I wasn’t able to find a well-written article on this topic also I’ve nothing to do right now so I’ll try to brief it here, just in case it helps anyone. The idea basically is to perform the 1D sliding window for both axes. Let me explain how exactly do we do it.
I think the basic idea is clear that we’ll store the time at which a particular cell is called and then iterate over all the cells of the grid and check if it has all A’s or all B’s (using 2D prefix sums as described above) and then take the minimum over the max value of each such K \times K submatrix(as max value is the operation number at which this submatrix became valid). So only catchy part is calculating the maximum value over K\times K sized submatrices so I’ll emphasize on it.
NOTATION:
- T_{i,j} → Operation number when cell (i,j) is filled by any of the players
- C_{i,j}=\max \{ T_{i-K+1,j},T_{i-K+2,j}\dots T_{i,j}\} → Max of last K elements of T in the same column as (i,j)
- S_{i,j}=\max\{C_{i,j-K+1},C_{i,j-K+2} \dots C_{i,j}\} → Max of last of last K elements of C in the same row as (i,j) .
2D SLIDING WINDOW:
So the first task at hand will be to calculate C_{i,j} for all cells which is defined above.
It could be easily calculated by iterating the grid column by column and maintaining a multiset of size K while iterating any particular column(which will basically store T_{i,j} values for all the cells shaded in black). The following block of code should make it clearer.
CODE
//1D Sliding window
for(int j=1;j<m+1;j++){
multiset<int>s ;
for(int i=1;i<k+1;i++)
s.insert(t[i][j]) ;
C[k][j]=*--s.end() ;
for(int i=k+1;i<n+1;i++){
s.erase(s.find(t[i-k][j])) ;
s.insert(t[i][j]) ;
C[i][j]=*--s.end() ;
}
}
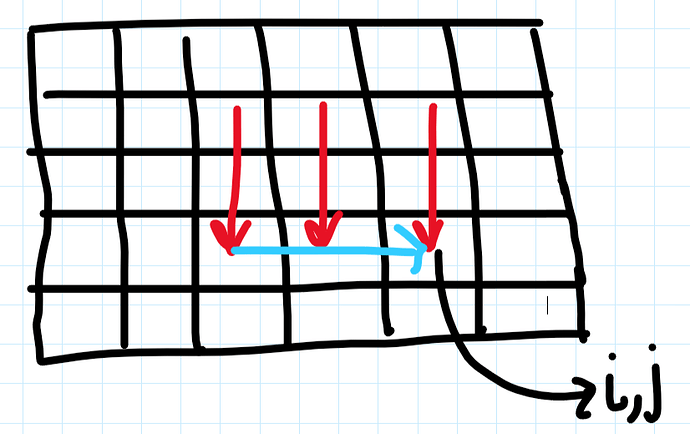
Once done with that now we’ll calculate S_{i,j} which will be calculated by in the exact same manner by iterating the grid row by row and storing C_{i,j} values in the multiset. It should now be obvious that S_{i,j} store the value of the maximum element present in the submatrix of size K \times K having its bottom right corner at (i,j). the following figure should add more intuition to it.
Red arrows depict the max taken during C_{i,j} calculation and blue arrow depicts the max taken during S_{i,j} calculation. We can see that we’ve covered the entire 3x3 grid ending at (i,j)
CODE
for(int i=1;i<n+1;i++){
multiset<int>s ;
for(int j=1;j<k+1;j++)
s.insert(C[i][j]) ;
S[i][k]=*--s.end() ;
for(int j=k+1;j<m+1;j++){
s.erase(s.find(cx[i][j-k])) ;
s.insert(cx[i][j]) ;
S[i][j]=*--s.end() ;
}
}
Now that we have max values over all submatrices of size K\times K and problem could be solved using 2D prefix sums described above.
IMPLEMENTATION:
CODE
#include "bits/stdc++.h"
using namespace std ;
void solve(){
int n,m,k ;
cin >> n >> m >> k ;
vector<vector<int>>a(n+1,vector<int>(m+1)),b(n+1,vector<int>(m+1)),t(n+1,vector<int>(m+1)),cx(n+1,vector<int>(m+1)),sx(n+1,vector<int>(m+1));
for(int j=0,x,y;j<n*m;j++){
cin >> x >> y ;
(j&1^1)?a[x][y]=1:b[x][y]=1 ;
t[x][y]=j ;
}
for(int j=1;j<m+1;j++){
multiset<int>s ;
for(int i=1;i<k+1;i++)
s.insert(t[i][j]) ;
cx[k][j]=*--s.end() ;
for(int i=k+1;i<n+1;i++){
s.erase(s.find(t[i-k][j])) ;
s.insert(t[i][j]) ;
cx[i][j]=*--s.end() ;
}
}
for(int i=1;i<n+1;i++){
multiset<int>s ;
for(int j=1;j<k+1;j++)
s.insert(cx[i][j]) ;
sx[i][k]=*--s.end() ;
for(int j=k+1;j<m+1;j++){
s.erase(s.find(cx[i][j-k])) ;
s.insert(cx[i][j]) ;
sx[i][j]=*--s.end() ;
}
}
for(int i=1;i<n+1;i++)
for(int j=1;j<m+1;j++){
a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1];
b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
}
auto get=[&](int x,int y,vector<vector<int>>&c){
return c[x][y]-c[x-k][y]-c[x][y-k]+c[x-k][y-k] ;
} ;
int ok=-1,v=1e9 ;
for(int i=k;i<n+1;i++){
for(int j=k;j<m+1;j++){
if(get(i,j,b)==k*k&&sx[i][j]<v)
ok=1,v=sx[i][j] ;
if(get(i,j,a)==k*k&&sx[i][j]<v)
ok=0,v=sx[i][j] ;
}
}
if(ok==-1){
cout<<"Draw\n" ;
return ;
}
cout << (ok?"Bob\n":"Alice\n") ;
}
signed main(){
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int TC ;
cin >>TC ;
while(TC--)
solve() ;
}
Do let me know if there’s something which isn’t clear.
I also missed the Binary Search. I implemented 2D prefix sum well but binary search was required in this question as per my solution.
We all know who is sus. Even if you check any 10 submissions, you can find at least 2-3 with same solution but I don’t know why codechef ignores that.
I am wondering if Codechef is using any plagiarism detector or they are just ignoring plagiarism so that they can publish result asap.
Here I’m using a simple idea that when someone performs a move, then the only chance that the K*K matrix form in on that cell in one of the four directions, and the rest is basic implementation.
Can someone look into this solution and tell me where I’m wrong or provide a test case? Also, there is something which I’m doing wrong, or might be a silly mistake, can anyone tell that?
https://www.codechef.com/viewsolution/48211471
Here is my solution without use of binary search and trees etc. It just failed to pass 3 test cases. Can you tell me where I was wrong. I am unable to find it out on my own. It would be really great help!
Thanks
Can someone please tell why is the 1st set getting passed by O((n*m)^2 * k^2). Because the number of test cases are 10^5 and n=10, m=10, k=10 in worst case, which makes total 10^11 operations, which should give TLE. TIA
If I’m understanding your post correctly, you’re presenting a scenario where T=10^5, N = 10 and M= 10.
I had same ques, does this statement change with subtask ?
If N=10 and M=10 then The sum of N*M should not exceed 100, right ?