Hey!. Let the base length is B. Since the triangle is right-angled isosceles, even the perpendicular is B. The angle between base and hypotenuse is 45 degrees.(tan theta = B/B = 1). Now we need to find the position on the base beyond which a square of 2 units cannot exist. Again from tan theta, this is 2. Therefore, squares can be drawn on B-2 space. Therefore number of squares = (B-2)/2 = B/2 - 1. These squares are on the base. The part left in perpendicular is B-2, which is again a right-angled isosceles triangle. Hope this helps!
Here is the recursive code (Python 3.6) :
def rec(b):
if b<4:
return 0
else:
return (b//2 - 1) + rec(b-2)
if __name__==‘__main__’:
for _ in range(int(input())):
print(rec(int(input())))
Here is the optimal code:
for _ in range(int(input())):
b = int(input())
if b<4:
print(0)
continue
else:
if b%2==1:
b-=1
print(((b-2)*(b))//8)Can you please help me with this, I am getting NZEC for the code,
def recursion(n):
if(n<4):
return 0
else:
return recursion(n-2)+(n//2)-1
for t in range(int(input())):
n = int(input())
print(recursion(n))
Why am I getting NZEC for this code?
def recursion(n):
if(n<4):
return 0
else:
return recursion(n-2)+(n//2)-1
for t in range(int(input())):
n = int(input())
print(recursion(n))
If n=10**4 (see constraints) then it will raise recursion error hence it is better to use mathematical approach than recursion one. Hope this helps. Happy coding! 
This solution is for a square of nxn.
Triangle base is B.
int main(){
int t, B; //no. of testcase and base of a triangle
int k, n;
cin>>t;
while (t–){
int result;
cin>>B;
k = B/n;
result = (k*(k-1))/2;
cout<<result<<endl;
}
}
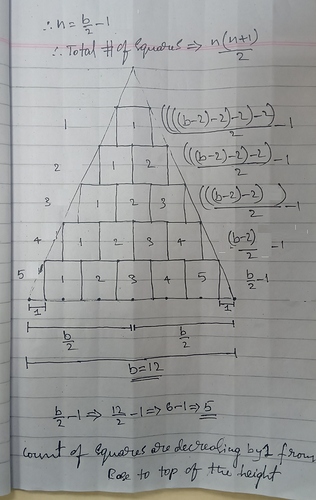
please explain clearly b/2-1 came from
how total no of squares is (b-2)/2 I understood till less than b-2 length only square is possible help me …
You should use recursion limit in Python, add following 2 lines top of your code :
import sys sys.setrecursionlimit(10**7)
VVGoodEditorial:p
CodeChef: Practical coding for everyone i am getting runtime error can anyone plz tell me what’s wrong in my code
simple solution:
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin>>t;
while(t–){
int B;cin>>B;
int N=(B/2)-1;
cout<<((N*(N+1))/2)<<endl;
}
return 0;
}
The triangle is not correct as it should be right angled.
How do we reach to f(B)=sum of first m natural nos and if it is so why is it m*(m-1)/2 shouldn’t it be m*(m+1)/2
Conditions about how the squares should be fit in should be much clearer. Based on the conditions given in question, if I over lap the squares, i.e by moving the squares by a infinitesimally small, I can always fit another square, making the number of squares that can fit in infinite. Hope someone clears the question.
how does the recusrsion statement give us f(b)=b/2+(b/2-1)+…+1
and how is it equal to sum of b/2 natural nos
Simplest/Fastest C++ Solution without even using Recursion:
#include <iostream>
using namespace std;
int main() {
int t,b,count;
cin>>t;
while(t--) {
count = 0;
cin>>b;
while(b>=2) {
b -= 2;
count += b/2;
}
cout<<count<<endl;
}
return 0;
}Nice. Greedy One !
Nice approach pal