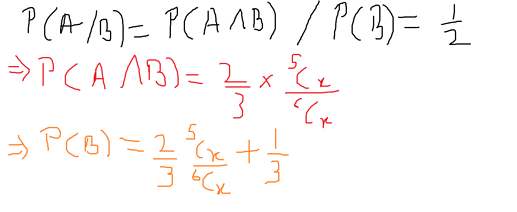So this was asked to me by one of my friend and is based on probability which I thing is Conditional \ Bayes Theorem.
You've 6 folders in your office where you store your documents (with equal probabilities).
But in 1/3 cases - you simply leave the documents in your home.
Today you need a document in your office & start searching your office folders.
How many folders you'd have checked after which you can conclude that that
the probability of finding that document in your office is 50%?
Can someone provide me a detailed solution to this problem. Thanks
@ssrivastava990 @galencolin @vijju123 @taran_1407
I’ve calculated the answer as 3 (not sure though)!!
Can you explain how you thought so ?
Are you sure 3 is correct? I am writing my logic.
No, there are no options. It was an interview question. So I don’t know final answer. Still you can guide me how to approach.
Is there only one document meaning out of 6 folders only 1 folder contains the document or there may be docs in multiple folders and you’ve to search for a particular doc?
I didn’t think this before…so my logic might be wrong. I’ll update after do it again.
No there will be one document only not docs.
So, here is my logic.
The answer is 3 (according to me)…
There are 6 folders in the office with equal probability to hold the doc. However, there is a 7th folder which can contain the doc with a probability 1/3.
So each of the six folders in the office have a 1/9 chance to contain the doc.
You search through one folder. You don’t find the doc. Now the probability of finding the doc in the office becomes \dfrac {5*1/9}{5*1/9 + 1/3} = 5/8.
Similiarly after searching through the second folder it becomes 4/7 .
And after the third folder, it becomes 3/6 = 1/2
2 Likes
This seem correct. The 7th folder that you are referring is home that can contain the folder with 1/3 probability. Right ? well explained. I think it is right.
A more general formula for finding the probability in case of n folders and a probability of p that the doc is at home after opening i folders
Pi = \dfrac {(n - i)*\dfrac{1-p}{n}}{(n - i)*\dfrac{1-p}{n} + p}
1 Like
Yes, the seventh folder refers to the probability of finding the doc at home.
1 Like
Then-
How many folders you'd have checked after which you can conclude that that the probability of finding that document in your office is 50%?
Let’s say he opened x folders and all the x folders should be empty as if any one contains that doc, the probability is 1.
Let A denotes the event that the doc is in office.
Let B denotes the event that he has opened x folders and all are empty.
We want P(A/B)=0.5
P(A/B)=\frac{P(A \cap B)}{P(B)}
Plug in the values and solve for
x.
x=3 satisfies above expression.
This is what I think (I may be wrong).
1 Like