PROBLEM LINK:
Setter: Arjun Arul
Editorialist: Samarth Gupta
DIFFICULTY:
Medium
PREREQUISITES:
Dynamic Programming
PROBLEM:
Given a floor of dimension K × N, where K =1, 2, 3, you need to cover the floor with tiles of size 2 × 2 or 3 × 1 or 1 × 3. Every cell of the floor should be covered by exactly one tile and all the tiles should lie within the floor. Find the number of ways of doing so.
QUICK EXPLANATION:
Handle cases K = 1, 2, 3 separately. Build a recurrence with different types of tiles and then compute the number of ways.
EXPLANATION:
Figures shown below are not drawn to scale.
K = 1
Since we have 1 × N dimension of the floor, if N \% 3 == 0, then we have 1 way, else there is no other way.
K = 2
Here we have 2 × N dimension of the floor, let dp[N] denotes the number of ways with which we can tile this floor. We have only 2 possibilities here:
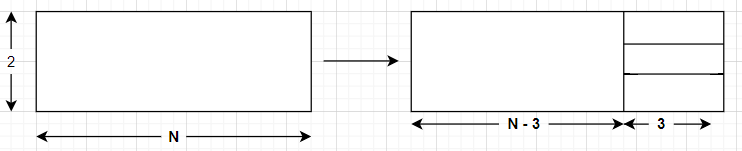
- Place a 2 × 2 tile as shown below:
- Place three 1 × 3 tiles as shown.
We can see that we cannot have any other case here, therefore the recursion of dp[N] would be dp[N] = dp[N-2] + dp[N-3]. Also, dp[1] = 0, dp[2] = 1, dp[3] = 1. We can find dp[N] in O(N) using this recursion.
K = 3
This is the toughest part. Let’s think it in the same way we thought for K = 2. Here we have 3 × N floor and we have 3 different types of tiles available. Can we convert the 3 × N floor problem to 3 × M problem where M < N by using some tiles? Well, it turns out that we cannot and we need some extra shapes in this case. Let’s first define the arrays we would need in this problem.
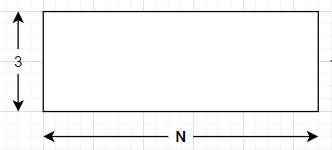
Let a[N] be the number of ways to cover the floor of size 3 × N using the tiles we have. Our answer would be a[N]. The figure for the same is:
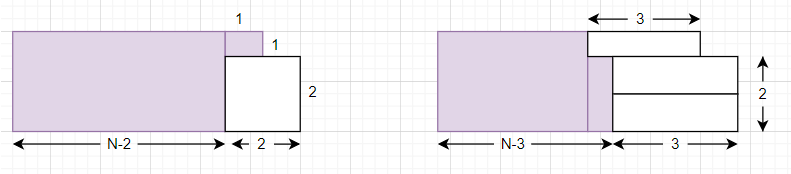
Let b[N] denote the number of ways to cover the shape shown below, a rectangle of dimension 3 × (N-1) with an extra 2 × 1 rectangle at the bottom right corner. You can see it is symmetric to the second figure shown below.

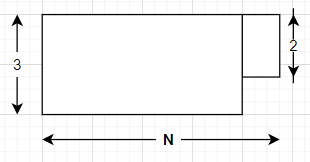
Let d[N] denote the number of ways to cover the shape shown below, a rectangle of dimension 3 × N with an extra 1 × 1 square at the top right corner. You can see it is symmetric to the second figure shown below.
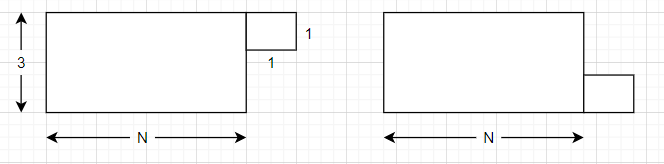
Now let’s see how to derive recursion for a[N], b[N], d[N].
Consider a[N], we have 4 ways to cover the floor as shown:
Note that colored tiles shows the states after removing some tiles. In the above figure we first use 1 × 3 tiles for first figure, then 3 × 1 tiles for second figure, and then a 2 × 2 square with a 1 × 3 tile for third and fourth figure. Note that last 2 are symmetrical. Therefore we have the recursion: a[N] = a[N-3]+a[N-1]+2*b[N-2].
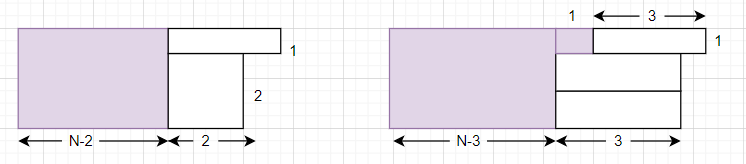
Consider b[N], we have 2 ways to cover the floor as shown:
Note that colored tiles shows the states after removing some tiles. In the first figure, we place a 2 × 2 tile at the bottom, and in the second case place two 1 × 3 tiles at the bottom and a 1 × 3 tile at the top. Here we have the recursion: b[N] = d[N-2]+b[N-3].
Consider d[N], we have 2 ways to cover the floor as shown:
Note that colored tiles shows the states after removing some tiles. In the first figure, we first 2 × 2 tile at bottom and 1 × 3 tile at the top. In the second figure, we place three 1 × 3 tiles. Here we have the recursion: d[N] = a[N-2]+d[N-3].
Using the above 3 recursions, we can compute a[N], b[N], d[N]. But we need the initial conditions. Try to think them on your own and check below.
Initial Conditions
a[0] = 1, b[0] = 0, d[0] = 0
a[1] = 1, b[1] = 0, d[1] = 0
a[2] = 1, b[2] = 0, d[2] = 1
So we can solve for K = 3 in O(N) also.
Overall Time Complexity : O(N)
SOLUTION:
Editorialist Solution
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define mod 1000000007
signed main() {
ios_base::sync_with_stdio(false);
cin.tie(0);
int t;
cin >> t;
while(t--)
{
int k, n;
cin >> k >> n;
if(k == 1)
{
if(n%3 == 0)
cout << 1 << '\n';
else
cout << 0 << '\n';
}
else if(k == 2)
{
int dp[n+5] = {0};
dp[1] = 0;
dp[2] = 1;
dp[3] = 1;
for(int i = 4;i < n+5;i++)
dp[i] = (dp[i-2] + dp[i-3])%mod;
cout << dp[n] << '\n';
}
else
{
int a[n+5] = {0}, b[n+5] = {0}, d[n+5] = {0};
a[0] = 1, b[0] = 0, d[0] = 0;
a[1] = 1, b[1] = 0, d[1] = 0;
a[2] = 1, b[2] = 0, d[2] = 1;
for(int i = 3; i < n+5;i++)
{
a[i] = (a[i-1] + a[i-3] + 2*b[i-2])%mod;
b[i] = (d[i-2] + b[i-3])%mod;
d[i] = (a[i-2] + d[i-3])%mod;
}
cout << a[n] << '\n';
}
}
}
BONUS PROBLEM:
Solve the 3 × N case when N = 10^{18}.
This is my first Editorial. Suggestions(if any) are most welcome ![]()
Also can anyone suggest some tool to draw better figures? @vijju123, @carre , @everule1