Recently I had participated in a contest on Hackerearth and came across this problem : Numbers Game
Problem Statement Summary
This is a game between two persons : Robert and Ned .
There are two numbers N and K provided to us.
Robert Starts and picks a number , say x between 1 and K
Ned then picks a number (let’s call the number y) between x+1 and x+K
Now Robert’s turn again and he picks a number between y+1 and y+K and so on and so forth.
The first person to reach N wins. Both persons play optimally
We must determine who will WIN this game !!
Sample Case Explanation
If N = 3 and K = 3 ,
Robert plays first and can choose a number between 1 and K , here he can choose 3 which is in fact N and ends up winning the game !
If N = 4 and K = 1 ,
Robert’s Turn : Has to pick between 1 and K , in this case , he can pick only 1 , Let us call this choice_1 = 1
Ned’s Turn : Has to pick between choice_1+1 and choice_1+K => In this case , 2 so
choice_2 = 2
Robert’s Turn : Has to pick between choice_2+1 and $choice_2+K =>$ 3 so choice_3 = 3
Ned’s Turn : By Similar Reasoning , choice_4 = 4 , which is actually N and game ends here making Ned the winner 
Try to think a bit on how you would approach it before moving forward !
My Approach , Thoughts and Observations
Initially of course , my head was pretty muddled up because this was a short contest requiring you to find the solution really quick and I did not know how to simulate the players playing optimally
I was stuck.
Then I started thinking of trivial cases , if K >= N , obviously in the first turn itself when Robert plays and has to select a number between 1 and K , he can select N and conclusively win there and then
Then I was fumbling a bit with the idea of N-K as I thought if a player got to / chose N-K in any move , the player in the next move will win as he can select N in the next move .
The third thing that caught my attention was the low constraints on N and K , both were under 1001 indicating that an O(N^2) solution would pass.
Now a solution started forming in my mind :
Let’s look at the numbers from back to front i.e. from N to 1 , I took the example of N=10 and K=3 so we look at the sequence of numbers
Let’s begin :
If some player is at the number 10 , He is the WINNER so the same person who obtains 10 is the winner . Next
If a player is at 9 or is forced to choose 9 , then the same player cannot win because obviously in the next turn the other player will choose 10 which is N as the next player is allowed to choose from 9+1 to 9+K => 10 to 13 so different or other player will win . Next
Say a player chooses 8 , then the next player who plays after him can choose between 8+1 and 8+K which is 9 to 11 range , he chooses 10 obv so next or different player wins . Next
If a player is at 7 , the next player after him can choose from 8 to 10 , so he chooses 10 and different or next player wins . Then
Now the real fun begins , if a player is at 6 , the next player can choose from 7 to 9 (From 6+1 to 6+K )
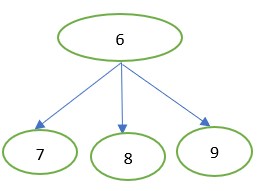Next player can choose b/w 7 to 9But we already know that if a player arrives at 7 , the other player will win
If a player arrives at 8 , the next / other / different player will win
If a player arrives or chooses 9 , other or next player will win
So if a player chooses 6 as we saw in the root node , no matter what the next player chooses , the same or original player , the one who chose 6 will WIN . Why ?
Let’s say Player A chooses 6
Player B chooses 7 then next turn Player A chooses 10
Player B chooses 8 then next turn Player A chooses 10
Player B chooses 9 then next turn Player A chooses 10
No matter what happens the original player who chose 6 (Be It Player A or B ) will WIN .
Next …
If some player chooses 5 will we lose/win ?
Let’s look at the choices the other player has
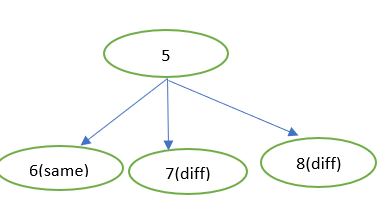
We know that if a player chooses 6 that player will win => same player
If a player chooses 7 , the other player will win
If a player chooses 8 , other player will win .
Now both of these players play optimally so if some player chooses 5 , the next player will look the options , 6 , 7 and 8 , he sees that if he chooses 6 , he wins so he takes that therefore the player who chooses 5 DOES NOT WIN i.e. the different player than the one who chose 5 wins .
Scenarios to prove
Player A chooses 5
Player B chooses 6
If Player A chooses 7 , 8 or 9 , in the next turn Player B can choose 10 and win .
Similar case when Player B chooses 5 , Player A chooses 6 , whatever Player B chooses , next turn Player A will win by choosing 10
The Player who chooses 5 DOES NOT WIN , the different or other player wins.
Similarly try by yourself to determine , if a player chooses 4 , does that same player win or different ?
and for 3 , 2 and 1
You will get this “result” array for indices 10 to 1 :
I denote 0 as same and 1 as different , as we’ve seen if a player gets to choose 10 , he wins so result[10] = 0
Similarly result[9] , result[8] , result[7] = 1 as the other player and not the player who chooses 7 , 8 , 9 wins and so on . Again the array is printed from index 10 to index 1
I just loop through this array from index 1 to K which is what Rob starts out with , if at least one SAME is present Rob wins else Ned wins i.e. if count of 0 in result array from indices 1 to K is greater than equal to 1 , then Rob WINS .
Why ? Because , if one of the value is same , then the guy who chooses that number , the same guy wins by our reasoning above !
Code
#include <bits/stdc++.h>
using namespace std ;
int main()
{
//0 denotes same and 1 denotes opposite
int t;
cin >> t ;
while(t--)
{
long long int n , k ;
int result[20000+1] ;
cin >> n >> k ;
//trivial case ?
if(k>=n)
cout << 0 << endl ;
else{
int same = 0 ;
for(int i=n ; i>=1 ; i--)
{
if(i==n)
result[i] = 0 ;
else if(i>=n-k && i<n)
result[i] = 1 ;
else
{
same = 0 ; //count of same
for(int sec = i+1 ; sec<=i+k ; sec++)
{
if(sec<=n && result[sec]==0)
same++ ;
}
if(same>=1)
result[i] = 1 ;
else
result[i] = 0;
}
}
same = 0 ;
for(int i=1 ; i<=k ; ++i)
{
if(i<=n && result[i]==0)
same++ ;
}
if(same>=1)
cout << 0 << endl;
else
cout << 1 << endl;
}
}
return 0 ;
}
And I got AC , I was so happy !!!
The question states to output 0 if Rob wins else 1 . The code above was the one I used in contest so it is not well documented and might be obfuscated . Let me know if I need to re-write a clean version will heavy comments if you don’t understand
Doubts
- Is my approach correct . I’ve read a lot of @tmwilliamlin’s comments about upsolving and trying questions that make you struggle and proving solutions and this question did make me struggle a bit and I was pretty happy instead of a pattern , I can justify why the solution worked
- Is there a faster way to solve this problem and how
- I know practise is the key to solving questions like these faster but what’s the most effective way to do guided practise on codechef
I’ve seen amazing coders like @ashishgup participate in this contest , it would be nice if they share their approaches
I’ve said it before that @viju123 and @ssjgz and now @tmwilliamlin are the best at this editorial business but I like to try my luck from time to time !
Let me know how it was .
- Enjoyed it ! Do more of these
- Hated It
0 voters
Cya Later!!
I’d better start solving game theory problems soon !