Hello @all,
This tutorial will cover the topic of Fast Modulo Multiplication (also known as Exponential Squaring or Repeated Squaring).
This is a very useful technique to have under your arsenal as a competitive programmer, especially because such technique often appears on Maths related problems and, sometimes, it might be the difference between having AC veredict or TLE veredict, so, for someone who still doesn’t know about it, I hope this tutorial will help ![]()
- Main reason why the usage of repeated squaring is useful
This technique might seem a bit too complicated at a first glance for a newbie, after all, say, we want to compute the number 310. We can simply write the following code and do a simple for loop:
#include <iostream>
using namespace std;
int main()
{
int base = 3;
int exp = 10;
int ans = 1;
for(int i = 1; i <= exp; i++)
{
ans *= base;
}
cout << ans;
return 0;
}
The above code will correctly compute the desired number, 59049. However, after we analyze it carefully, we will obtain an insight which will be the key to develop a faster method.
Apart from being correct, the main issue with the above method is the number of multiplications that are being executed.
We see that this method executes exactly exp-1 multiplications to compute the number nexp, which is not desirable when the value of exp is very large.
Usually, on contest problems, the idea of computing large powers of a number appears coupled with the existence of a modulus value, i.e., as the values being computed can get very large, very fast, the value we are looking to compute is usually something of the form:
nexp % M ,
where M is usually a large prime number (typically, 109 + 7).
Note that we could still use the modulus in our naive way of computing a large power: we simply use modulus on all the intermediate steps and take modulus at the end, to ensure every calculation is kept within the limit of “safe” data-types.
- The fast-exponentiation method: an implementation in C++
It is possible to find several formulas and several ways of performing fast exponentiation by searching over the internet, but, there’s nothing like implementing them on our own to get a better feel about what we are doing ![]()
I will describe here the most naive method of performing repeated squaring. As found on Wikipedia, the main formula is:
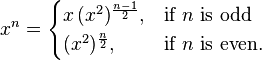
A brief analysis of this formula (an intuitive analysis if you prefer), based both on its recursive formulation and on its implementation allows us to see that the formula uses only O(log2n) squarings and O(log2n) multiplications!
This is a major improvement over the most naive method described in the beginning of this text, where we used much more multiplication operations.
Below, I provide a code which computes baseexp % 1000000007, based on wikipedia formula:
long long int fast_exp(int base, int exp)
{
if(exp==1)
return base;
else
{
if(exp%2 == 0)
{
long long int base1 = pow(fast_exp(base, exp/2),2);
if(base1 >= 1000000007)
return base1%1000000007;
else
return base1;
}
else
{
long long int ans = (base* pow(fast_exp(base,(exp-1)/2),2));
if(ans >= 1000000007)
return ans%1000000007;
else
return ans;
}
}
}
- The 2k-ary method for repeated squaring
Besides the recursive method detailed above, we can use yet another insight which allows us to compute the value of the desired power.
The main idea is that we can expand the exponent in base 2 (or more generally, in base 2k, with k >= 1) and use this expansion to achieve the same result as above, but, this time, using less memory.
Below you can find the code provided in the comment by @michal27:
ll fast_exp(int base, int exp) {
ll res=1;
while(exp>0) {
if(exp%2==1) res=(res*base)%MOD;
base=(base*base)%MOD;
exp/=2;
}
return res%MOD;
}
These are the two most common ways of performing repeated squaring on a live contest and I hope you have enjoyed this text and have found it useful ![]()
- Useful problems to practice this new concept:
- Further analysis and generalizations
Besides the simple method explained here, applied only to the computation of large powers of a given number, it turns out that this method is widely used in the fast computation of powers of matrices and, as we shall see on a later tutorial (hopefully, not so later ![]() ) this is where this method actually excels and provides really good methods for tackling hard problems
) this is where this method actually excels and provides really good methods for tackling hard problems ![]()
Best regards,
Bruno

