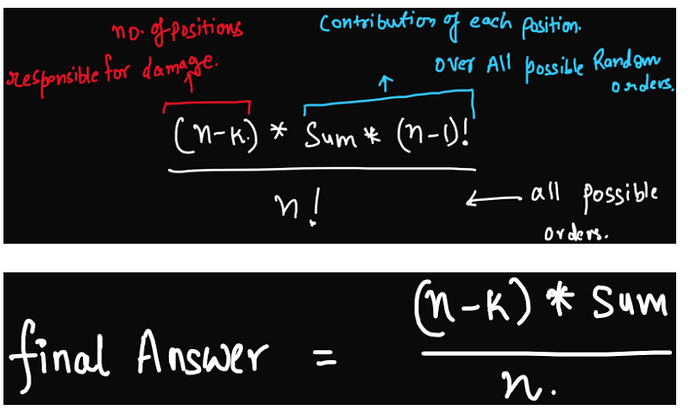
Let us find the contribution of each friction damage over all possible orders.
If we fix position i to contain some value of friction f, then the contribution of friction f in this arrangement would be f*(n-1)!. Since we can fix the position to contain any of the values of f, the net contribution for fixing f’s on a certain position turns out to be f1*(n-1)! + f2*(n-1)!..=(summation over all frictions ) * (n-1)!
If the power of the engine is k, then no damage must be incurred in the first k positions, only the last n-k positions will be responsible for the damage. Thus, the total number of arrangements in which a particular friction can be assigned is f*(n-k)(n-1)!. Hence, the total answer will be summation over all frictions i.e. (summation over all frictions ) * (n-1)!(n-k)
Divide by n! for multiplying the probability factor in the expected value.
Code Link : Code