PROBLEM LINK:
Practice
Contest: Division 1
Contest: Division 2
Setter: Alei Reyes
Tester: Aleksa Plavsic
Editorialist: Taranpreet Singh
DIFFICULTY:
Easy-Medium
PREREQUISITES:
Case-based Analysis and Basic Math would be sufficient.
PROBLEM:
Given starting position (r,c) of the bishop in a N*M chessboard, Find the number of distinct squares that can be visited within K moves.
A bihsop from position (r,c) can move to any cell (r`, c`) satisfying either r+c = r`+c` or r-c = r`-c`.
SUPER QUICK EXPLANATION
- Handle K = 1 case separately. Answer in this case is just 1+min(r-1,c-1)+min(r-1, m-c)+min(n-r,c-1)+min(n-r,m-c).
- For every K \geq 2, The reachable positions will form be of form some rectangles followed by a triangle on both sides of (r,c). Calculate the number of cells in squares and triangles separately.
- For simplicity, we can solve two smaller instances, by splitting the board into two parts, first of dimension N*C which lies left to position (r,c) and other of dimensions N*(M-C+1) lying right to the position of bishop. We can now see, that bishop lie in the first column always, simplifying our implementation.
- If you split the board, remember not to overcount the reachable cells in c th column since that column will appear in both boards.
EXPLANATION
So, let’s begin another combinatorics problem. I am assuming you all are familiar with bishop movement in chess.
First of all, we will separately solve the case where K = 1.
In this case, only the cells which lie on the same diagonal as the current position can be visited at all. This way, we just need to count the number of positions on board which lie on that diagonal. We can split each diagonal into two parts resulting in four diagonal segments, namely upper left diagonal, upper right diagonal, lower left diagonal and lower right diagonal.
We can see, that we can move at most min(r-1, c-1) steps in the upper-left direction since we will hit either top border or left border after this many steps. Similarly, we can move at most min(r-1, m-c) steps in the upward-right direction. We can similarly find for lower two directions.
Also, the intial position is also considered reachable, so adding 1 to answer, getting the expression 1+min(r-1, c-1)+min(r-1, m-c)+min(n-r,c-1)+min(n-r,m-c) as answer for K = 1.
Now, assume K \geq 2.
Let’s assume that the initial position of bishop is (1,1). Now, we can try out some examples to find out pattern occurring.
For N = 5, M = 19, K = 2.

For N = 5, M = 19, K = 3.

For N = 5, M = 19, K = 4.

Try to make a pattern first, and after giving a try, continue.
If we observe carefully, we can see that ignoring the first column, we have exactly K-1 rectangles of length N-1 and height N, followed by a triangle with width N-1 and height N-1 as highlighted in the image.

We can calculate the number of cells of the same color in the red rectangle and green triangle separately.
Now consider one case where starting position lies in the first column (not necessarily in the first row).

After observing, we may see that there is the same pattern, K-1 rectangles of N-1 width and N height, but followed by 2 triangles, as shown below.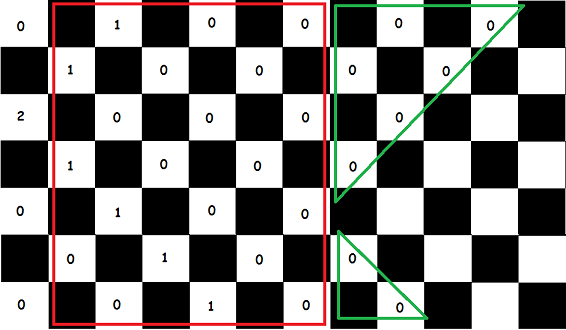
We can calculate the number of reachable positions in triangles as well as red rectangles. Add to it the number of reachable positions in the first column, to get the number of reachable positions in the whole board.
Sometimes, it may happen, that either the triangle doesn’t occur at all when rectangles itself cover the whole board, or the triangle may occur partially. Handle these cases carefully.
See the following image.

Triangle get’s cropped due to reaching the right end.
This way, we can calculate the number of reachable positions when the initial position lies in the first column, and add to it the number of reachable positions in the first column, which we ignored earlier.
Now, returning to the original problem, we can just apply the same trick.
Just divide the board into two parts of the same height, one with first C columns while other with M-C+1 columns. We see that Number of reachable positions in the original board is just number of reachable positions in both new boards less number of reachable positions in Cth column since it gets included in both.
Now, the problem gets reduced to just two smaller problems we just solved.
The Key thing, is, count the number of positions having the same color in a region (especially in triangles) carefully.
For implementation, feel free to refer the solutions below, after giving a try.
Time Complexity
Time complexity per test case should be O(1) since we calculate everything in constant time by Arithmetic operations only.
AUTHOR’S AND TESTER’S SOLUTIONS:
Setter’s solution
Tester’s solution
Feel free to Share your approach, If it differs. Suggestions are always welcomed. ![]()