PROBLEM LINK:
Author: Alei Reyes
Tester: Suchan Park
Editorialist: William Lin
DIFFICULTY:
Simple
PREREQUISITES:
Constructive algorithms
PROBLEM:
A bishop starts on a black cell on a chessboard. Find a sequence of at most 64 moves so that the bishop can visit all black cells on the board.
QUICK EXPLANATION:
We can visit all cells in a single diagonal of the board by moving to the topmost and bottommost cell of the diagonal. After we visit all diagonals, we will have visited all cells on the board.
EXPLANATION:
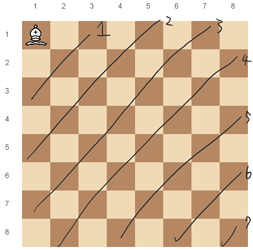
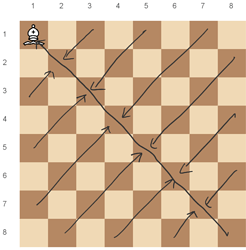
Let’s solve the first subtask first. The bishop starts at (1, 1). Our plan is to cover the diagonals one by one:
To visit the next diagonal, we first move down and right by one cell. Then, we move to the topmost cell of the diagonal and the bottommost cell of the diagonal in order to visit all cells of the diagonal. Before moving on to the next diagonal, we move back to the middle of the diagonal.
Implementation
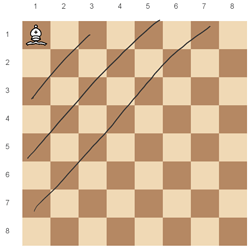
There are two parts to this. The first part deals with these diagonals:
for(int i=4; i<=8; i+=2) {
//visit all cells in x+y=i
}
First, we move to the middle of the new diagonal. If x+y=i, then x=y=\frac{i}{2}. Second, we move to the topmost cell of the diagonal, which is the cell in row 1. We can find the column to be (x+y)-x=i-1. Third, we move to the bottommost cell of the diagonal, which is the cell in column 1, and similarly, it is at (i-1, 1). Lastly, we move back to the middle of the diagonal, which is still (\frac{i}{2}, \frac{i}{2}).
for(int i=4; i<=8; i+=2) {
//visit all cells in x+y=i
//move to (i/2, i/2)
//move to (1, i-1)
//move to (i-1, 1)
//move to (i/2, i/2)
}
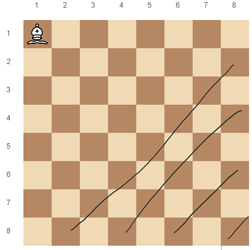
The second part is the last 4 diagonals:
The only change is that the topmost cell is the cell at column 8 and the bottommost cell is the cell at row 8.
for(int i=10; i<=16; i+=2) {
//visit all cells in x+y=i
//move to (i/2, i/2)
//move to (i-8, 8)
//move to (8, i-8)
//move to (i/2, i/2)
}
For subtask 2, the bishop can start on any cell, but we can easy use our solution for subtask 1 to solve this. We will somehow move our bishop to (1, 1), then perform the same solution for subtask 1.
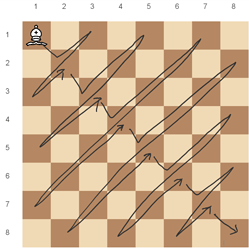
To move to (1, 1), we will first move to the diagonal (i, i), and then move to (1, 1), as shown here:
Implementation
The diagonal is represented by the line y=x, whereas the line of cells that the bishop can move to is y=-(x-r)+c. Solving the equations, we find that x=y=\frac{r+c}{2}. So our first two moves will be (\frac{r+c}{2}, \frac{r+c}{2}) and (1, 1).
SOLUTIONS:
Setter's Solution
#include<bits/stdc++.h>
using namespace std;
typedef long long int uli;
int rint(char nxt){
char ch=getchar();
int v=0;
int sgn=1;
if(ch=='-')sgn=-1;
else{
assert('0'<=ch&&ch<='9');
v=ch-'0';
}
while(true){
ch=getchar();
if('0'<=ch && ch<='9')v=v*10+ch-'0';
else{
assert(ch==nxt);
break;
}
}
return v*sgn;
}
int main(){
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
int t=rint('\n');
assert(1<=t&&t<=32);
while(t--){
int r=rint(' ');
int c=rint('\n');
assert(1<=r&&r<=8);
assert(1<=c&&c<=8);
assert((r+c)%2==0);
vector<pair<int,int> >ans={{r,c}};
int mid=(r+c)/2;
ans.push_back({mid,mid});
ans.push_back({1,1});
for(r=2;r<=4;r++){
ans.push_back({r,r});
ans.push_back({1,r+r-1});
ans.push_back({r+r-1,1});
ans.push_back({r,r});
}
for(r=5;r<=8;r++){
int x=2*(r-4);
ans.push_back({r,r});
ans.push_back({x,8});
ans.push_back({8,x});
ans.push_back({r,r});
}
printf("%d\n",int(ans.size()));
for(auto p:ans){
printf("%d %d\n",p.first,p.second);
}
}
assert(getchar()==EOF);
return 0;
}
Tester's Solution
//
// Created by ��찬 on 2020/02/22.
//
#include <bits/stdc++.h>
namespace {
const int BUFFER_SIZE = int(1.1e5);
char _buf[BUFFER_SIZE + 10];
int _buf_pos, _buf_len;
char seekChar() {
if(_buf_pos >= _buf_len) {
_buf_len = fread(_buf, 1, BUFFER_SIZE, stdin);
_buf_pos = 0;
}
assert(_buf_pos < _buf_len);
return _buf[_buf_pos];
}
bool seekEof() {
if(_buf_pos >= _buf_len) {
_buf_len = fread(_buf, 1, BUFFER_SIZE, stdin);
_buf_pos = 0;
}
return _buf_pos >= _buf_len;
}
char readChar() {
char ret = seekChar();
_buf_pos++;
return ret;
}
int readInt(int lb, int rb) {
char c = readChar();
int mul = 1;
if(c == '-') {
c = readChar();
mul = -1;
}
assert(isdigit(c));
long long ret = c - '0';
char first_digit = c;
int len = 0;
while(!seekEof() && isdigit(seekChar()) && ++len <= 19) {
ret = ret * 10 + readChar() - '0';
}
ret *= mul;
if(len >= 2) assert(first_digit != '0');
assert(len <= 18);
assert(lb <= ret && ret <= rb);
return (int)ret;
}
void readEoln() {
char c = readChar();
assert(c == '\n');
}
void readSpace() {
assert(readChar() == ' ');
}
}
bool gph[64][64];
std::vector<int> path;
bool vis[64];
bool brute(int u, int c) {
if(c == 32) {
printf("%ld\n", path.size());
for(int it : path) {
printf("%d %d\n", it / 8 + 1, it % 8 + 1);
}
return true;
}
for(int v = 0; v < 64; v++) if(!vis[v] && gph[u][v]) {
path.push_back(v); vis[v] = true;
if(brute(v, c+1)) return true;
path.pop_back(); vis[v] = false;
}
return false;
}
void run() {
int r = readInt(1, 8);
readSpace();
int c = readInt(1, 8);
readEoln();
r -= 1;
c -= 1;
assert((r + c) % 2 == 0);
memset(vis, 0, sizeof vis);
int u = r * 8 + c;
path.clear();
vis[u] = true;
assert(brute(u, 1));
}
int main() {
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
#endif
int T = readInt(1, 32);
readEoln();
for(int r1 = 0; r1 < 8; r1++) {
for(int c1 = 0; c1 < 8; c1++) {
int u = r1 * 8 + c1;
for(int r2 = 0; r2 < 8; r2++) {
for(int c2 = 0; c2 < 8; c2++) {
int v = r2 * 8 + c2;
if(r1 + c1 == r2 + c2 || r1 - c1 == r2 - c2) {
gph[u][v] = true;
}
}
}
}
}
while(T--) {
run();
}
return 0;
}
Editorialist's Solution
#include <bits/stdc++.h>
using namespace std;
void solve() {
//input
int r, c;
cin >> r >> c;
vector<array<int, 2>> moves;
//move to y=x diagonal
moves.push_back({(r+c)/2, (r+c)/2});
//move to (1, 1)
moves.push_back({1, 1});
//first 3 diagonals
for(int i=4; i<=8; i+=2) {
//visit all cells in x+y=i
moves.push_back({i/2, i/2});
moves.push_back({1, i-1});
moves.push_back({i-1, 1});
moves.push_back({i/2, i/2});
}
//last 4 diagonals
for(int i=10; i<=16; i+=2) {
//visit all cells in x+y=i
moves.push_back({i/2, i/2});
moves.push_back({i-8, 8});
moves.push_back({8, i-8});
moves.push_back({i/2, i/2});
}
//output
cout << moves.size() << "\n";
for(array<int, 2> a : moves)
cout << a[0] << " " << a[1] << "\n";
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
Please give me suggestions if anything is unclear so that I can improve. Thanks ![]()